5 - Inserción en AVL

Insertar en un AVL combina el recorrido de un BST con pasos extra de balanceo. Tras colocar la nueva clave, se recalculan alturas y se corrige cualquier desbalance usando las rotaciones LL, RR, LR o RL descritas en el tema anterior. El objetivo es conservar altura O(log n) aun con datos adversos.

vizualizador de arbol AVL

5.1 Inserción normal tipo BST

El primer tramo repite la lógica de un árbol de búsqueda: bajar por izquierda si la clave es menor, derecha si es mayor. No se permiten duplicados para simplificar.

  • Si el nodo actual es nulo, se crea una nueva hoja con altura 0.
  • Si la clave ya existe, se devuelve el nodo sin cambios.
  • El enlace de retorno conecta la subllamada al hijo correspondiente.

5.2 Actualización de alturas

Al volver de la recursión, cada nodo recalcula su altura usando las alturas de sus hijos. Esto prepara el dato para evaluar el factor de balance en O(1).

  • Altura de nodo nulo: -1.
  • Altura de nodo: 1 + max(alturaIzq, alturaDer).
  • Se actualiza desde el nodo hijo hacia la raíz.

5.3 Detección de desbalance

El factor de balance (FB) es la resta entre la altura izquierda y la derecha. Si |FB| > 1, el nodo está desbalanceado y requiere una rotación que dependen del signo de FB y del subárbol donde se insertó la clave.

  • FB > 1 implica exceso a la izquierda; FB < -1, exceso a la derecha.
  • El signo del FB del hijo afectado indica si es un caso simple (LL o RR) o doble (LR o RL).
  • El ajuste se hace localmente: rotar el nodo actual y devolver el nuevo subárbol equilibrado.

5.4 Casos LL, RR, LR y RL

El algoritmo completa la inserción aplicando la rotación correcta según la posición de la clave insertada:

def insertar_avl(nodo, clave):
  if not nodo:
    return crear_nodo_avl(clave)

  if clave < nodo.clave:
    nodo.izquierdo = insertar_avl(nodo.izquierdo, clave)
  elif clave > nodo.clave:
    nodo.derecho = insertar_avl(nodo.derecho, clave)
  else:
    return nodo  # duplicado: no se inserta

  actualizar_altura(nodo)
  fb = factor_balance_avl(nodo)

  # LL
  if fb > 1 and clave < nodo.izquierdo.clave:
    return rotar_derecha(nodo)
  # RR
  if fb < -1 and clave > nodo.derecho.clave:
    return rotar_izquierda(nodo)
  # LR
  if fb > 1 and clave > nodo.izquierdo.clave:
    nodo.izquierdo = rotar_izquierda(nodo.izquierdo)
    return rotar_derecha(nodo)
  # RL
  if fb < -1 and clave < nodo.derecho.clave:
    nodo.derecho = rotar_derecha(nodo.derecho)
    return rotar_izquierda(nodo)

  return nodo

Notas prácticas:

  • La función supone helpers previos: crearNodoAvl, actualizarAltura, factorBalanceAvl, rotarDerecha y rotarIzquierda de los temas anteriores.
  • Si se permiten duplicados, se puede definir una regla (por ejemplo, ir siempre a la derecha) y adaptar las condiciones de casos LR/RL acorde al subárbol usado.
  • Tras cada rotación se devuelven las nuevas raíces de subárbol; no olvide asignarlas al padre en el llamado recursivo.

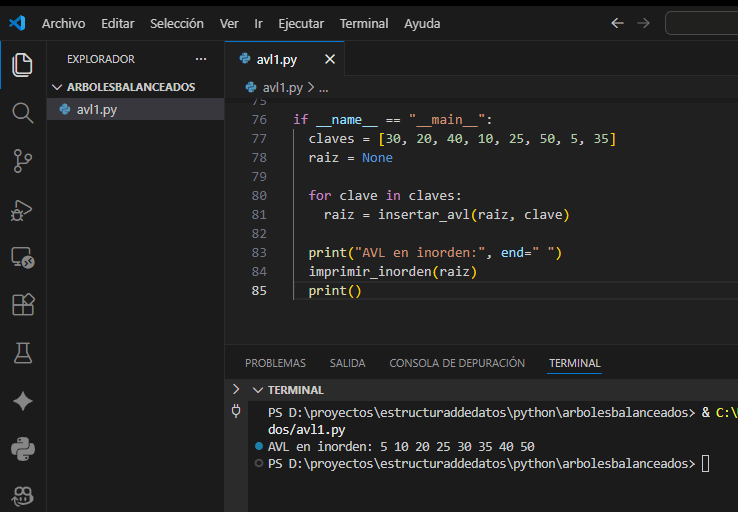
5.5 Código completo para probar en Python

Ejemplo autocontenible con inserciones y recorrido inorden. Copia y ejecuta.

class AvlNode:
  def __init__(self, clave):
    self.clave = clave
    self.altura = 0
    self.izquierdo = None
    self.derecho = None

def altura_nodo_avl(nodo):
  return nodo.altura if nodo else -1

def actualizar_altura(nodo):
  if not nodo:
    return
  h_izq = altura_nodo_avl(nodo.izquierdo)
  h_der = altura_nodo_avl(nodo.derecho)
  nodo.altura = 1 + max(h_izq, h_der)

def factor_balance_avl(nodo):
  if not nodo:
    return 0
  return altura_nodo_avl(nodo.izquierdo) - altura_nodo_avl(nodo.derecho)

def crear_nodo_avl(clave):
  return AvlNode(clave)

def rotar_derecha(y):
  x = y.izquierdo
  t2 = x.derecho
  x.derecho = y
  y.izquierdo = t2
  actualizar_altura(y)
  actualizar_altura(x)
  return x

def rotar_izquierda(y):
  x = y.derecho
  t2 = x.izquierdo
  x.izquierdo = y
  y.derecho = t2
  actualizar_altura(y)
  actualizar_altura(x)
  return x

def insertar_avl(nodo, clave):
  if not nodo:
    return crear_nodo_avl(clave)
  if clave < nodo.clave:
    nodo.izquierdo = insertar_avl(nodo.izquierdo, clave)
  elif clave > nodo.clave:
    nodo.derecho = insertar_avl(nodo.derecho, clave)
  else:
    return nodo

  actualizar_altura(nodo)
  fb = factor_balance_avl(nodo)

  if fb > 1 and clave < nodo.izquierdo.clave:  # LL
    return rotar_derecha(nodo)
  if fb < -1 and clave > nodo.derecho.clave:  # RR
    return rotar_izquierda(nodo)
  if fb > 1 and clave > nodo.izquierdo.clave:  # LR
    nodo.izquierdo = rotar_izquierda(nodo.izquierdo)
    return rotar_derecha(nodo)
  if fb < -1 and clave < nodo.derecho.clave:  # RL
    nodo.derecho = rotar_derecha(nodo.derecho)
    return rotar_izquierda(nodo)
  return nodo

def imprimir_inorden(nodo):
  if not nodo:
    return
  imprimir_inorden(nodo.izquierdo)
  print(nodo.clave, end=" ")
  imprimir_inorden(nodo.derecho)

if __name__ == "__main__":
  claves = [30, 20, 40, 10, 25, 50, 5, 35]
  raiz = None

  for clave in claves:
    raiz = insertar_avl(raiz, clave)

  print("AVL en inorden:", end=" ")
  imprimir_inorden(raiz)
  print()
Editor online
Visualización de un árbol AVL equilibrado
Retornar