6 - Eliminación en AVL
Eliminar en un AVL combina la lógica de un BST con una pasada extra para restaurar el balance. Tras desconectar el nodo, se recalculan alturas, se detectan desbalances y se aplican las rotaciones LL, RR, LR o RL que correspondan.
6.1 Eliminación tipo BST
- Se busca la clave bajando por izquierda o derecha según corresponda.
- Si el nodo tiene un hijo o ninguno, se reemplaza por su hijo existente (o por
NULL). - Si tiene dos hijos, se toma el sucesor inorden (mínimo del subárbol derecho), se copia su clave y luego se elimina el sucesor.
6.2 Ajustes posteriores
Al volver de la recursión, cada nodo recalcula su altura con la fórmula conocida 1 + max(alturaIzq, alturaDer). Esta actualización es necesaria para que el factor de balance quede consistente antes de revisar un posible desbalance.
6.3 Detección de desbalance
- Se calcula el factor de balance (FB) del nodo actual.
- Si
FBqueda fuera de [-1, 1], el subárbol necesita una rotación. - Para elegir el caso correcto se mira el signo del FB y del FB del hijo más alto.
6.4 Rotaciones de reequilibrio
La combinación de signos determina la rotación:
- LL: FB > 1 y el FB del hijo izquierdo ≥ 0. Rotación simple a la derecha.
- LR: FB > 1 y el FB del hijo izquierdo < 0. Rotación izquierda en el hijo, luego derecha.
- RR: FB < -1 y el FB del hijo derecho ≤ 0. Rotación simple a la izquierda.
- RL: FB < -1 y el FB del hijo derecho > 0. Rotación derecha en el hijo, luego izquierda.
class AvlNode:
def __init__(self, clave):
self.clave = clave
self.altura = 0
self.izquierdo = None
self.derecho = None
def altura_nodo(nodo):
return nodo.altura if nodo else -1
def min_nodo(nodo):
actual = nodo
while actual and actual.izquierdo:
actual = actual.izquierdo
return actual
def factor_balance(nodo):
if not nodo:
return 0
return altura_nodo(nodo.izquierdo) - altura_nodo(nodo.derecho)
def eliminar_avl(raiz, clave):
if not raiz:
return None
if clave < raiz.clave:
raiz.izquierdo = eliminar_avl(raiz.izquierdo, clave)
elif clave > raiz.clave:
raiz.derecho = eliminar_avl(raiz.derecho, clave)
else:
if not raiz.izquierdo or not raiz.derecho:
return raiz.izquierdo if raiz.izquierdo else raiz.derecho
succ = min_nodo(raiz.derecho)
raiz.clave = succ.clave
raiz.derecho = eliminar_avl(raiz.derecho, succ.clave)
raiz.altura = 1 + max(altura_nodo(raiz.izquierdo), altura_nodo(raiz.derecho))
fb = factor_balance(raiz)
if fb > 1 and factor_balance(raiz.izquierdo) >= 0:
return rotar_derecha(raiz) # LL
if fb > 1 and factor_balance(raiz.izquierdo) < 0:
raiz.izquierdo = rotar_izquierda(raiz.izquierdo)
return rotar_derecha(raiz) # LR
if fb < -1 and factor_balance(raiz.derecho) <= 0:
return rotar_izquierda(raiz) # RR
if fb < -1 and factor_balance(raiz.derecho) > 0:
raiz.derecho = rotar_derecha(raiz.derecho)
return rotar_izquierda(raiz) # RL
return raiz6.5 Código completo para probar en Python
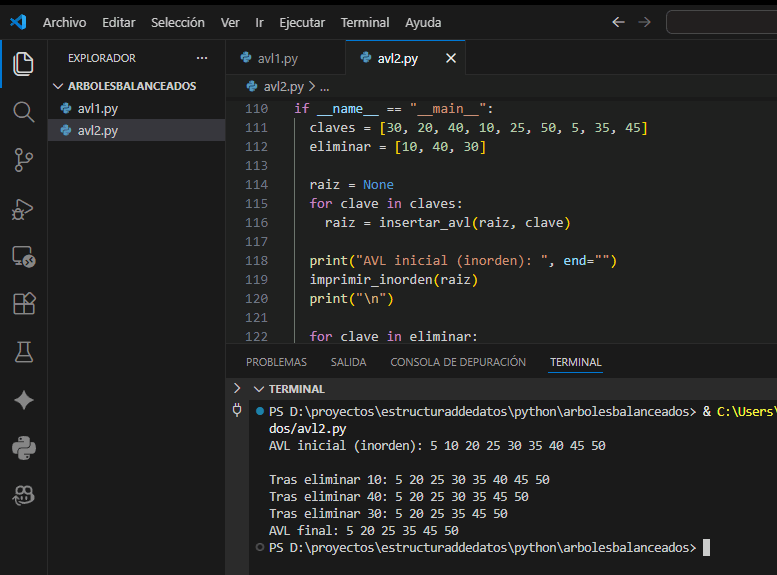
Ejemplo autocontenible que inserta, elimina claves y muestra el inorden antes y después. Copia y ejecuta.
class AvlNode:
def __init__(self, clave):
self.clave = clave
self.altura = 0
self.izquierdo = None
self.derecho = None
def altura_nodo(nodo):
return nodo.altura if nodo else -1
def actualizar_altura(nodo):
if not nodo:
return
nodo.altura = 1 + max(altura_nodo(nodo.izquierdo), altura_nodo(nodo.derecho))
def factor_balance(nodo):
if not nodo:
return 0
return altura_nodo(nodo.izquierdo) - altura_nodo(nodo.derecho)
def rotar_derecha(y):
x = y.izquierdo
t2 = x.derecho
x.derecho = y
y.izquierdo = t2
actualizar_altura(y)
actualizar_altura(x)
return x
def rotar_izquierda(y):
x = y.derecho
t2 = x.izquierdo
x.izquierdo = y
y.derecho = t2
actualizar_altura(y)
actualizar_altura(x)
return x
def crear_nodo(clave):
return AvlNode(clave)
def min_nodo(nodo):
actual = nodo
while actual and actual.izquierdo:
actual = actual.izquierdo
return actual
def insertar_avl(raiz, clave):
if not raiz:
return crear_nodo(clave)
if clave < raiz.clave:
raiz.izquierdo = insertar_avl(raiz.izquierdo, clave)
elif clave > raiz.clave:
raiz.derecho = insertar_avl(raiz.derecho, clave)
else:
return raiz
actualizar_altura(raiz)
fb = factor_balance(raiz)
if fb > 1 and clave < raiz.izquierdo.clave: # LL
return rotar_derecha(raiz)
if fb < -1 and clave > raiz.derecho.clave: # RR
return rotar_izquierda(raiz)
if fb > 1 and clave > raiz.izquierdo.clave: # LR
raiz.izquierdo = rotar_izquierda(raiz.izquierdo)
return rotar_derecha(raiz)
if fb < -1 and clave < raiz.derecho.clave: # RL
raiz.derecho = rotar_derecha(raiz.derecho)
return rotar_izquierda(raiz)
return raiz
def eliminar_avl(raiz, clave):
if not raiz:
return None
if clave < raiz.clave:
raiz.izquierdo = eliminar_avl(raiz.izquierdo, clave)
elif clave > raiz.clave:
raiz.derecho = eliminar_avl(raiz.derecho, clave)
else:
if not raiz.izquierdo or not raiz.derecho:
return raiz.izquierdo if raiz.izquierdo else raiz.derecho
succ = min_nodo(raiz.derecho)
raiz.clave = succ.clave
raiz.derecho = eliminar_avl(raiz.derecho, succ.clave)
actualizar_altura(raiz)
fb = factor_balance(raiz)
if fb > 1 and factor_balance(raiz.izquierdo) >= 0: # LL
return rotar_derecha(raiz)
if fb > 1 and factor_balance(raiz.izquierdo) < 0: # LR
raiz.izquierdo = rotar_izquierda(raiz.izquierdo)
return rotar_derecha(raiz)
if fb < -1 and factor_balance(raiz.derecho) <= 0: # RR
return rotar_izquierda(raiz)
if fb < -1 and factor_balance(raiz.derecho) > 0: # RL
raiz.derecho = rotar_derecha(raiz.derecho)
return rotar_izquierda(raiz)
return raiz
def imprimir_inorden(nodo):
if not nodo:
return
imprimir_inorden(nodo.izquierdo)
print(nodo.clave, end=" ")
imprimir_inorden(nodo.derecho)
if __name__ == "__main__":
claves = [30, 20, 40, 10, 25, 50, 5, 35, 45]
eliminar = [10, 40, 30]
raiz = None
for clave in claves:
raiz = insertar_avl(raiz, clave)
print("AVL inicial (inorden): ", end="")
imprimir_inorden(raiz)
print("\n")
for clave in eliminar:
raiz = eliminar_avl(raiz, clave)
print(f"Tras eliminar {clave}: ", end="")
imprimir_inorden(raiz)
print()
print("AVL final: ", end="")
imprimir_inorden(raiz)
print()