9 - Inserción en Red-Black Tree

Insertar en un Red-Black Tree comienza como un BST normal y luego aplica recoloreo y rotaciones para evitar dos rojos consecutivos y conservar la misma cantidad de nodos negros en cada camino.

vizualizador de arbol Red-Black

9.1 Inserción como BST

El primer paso es idéntico a un árbol de búsqueda binaria:

  • Recorrer por izquierda si la clave es menor, derecha si es mayor.
  • Si la clave ya existe, se puede devolver el nodo y no insertar duplicados.
  • Al llegar a una hoja NIL, se crea el nuevo nodo enlazándolo donde corresponda.

9.2 Colorear nodo inicial

El nodo recién creado se pinta rojo; esto evita incrementar la altura negra. Excepción: si es la raíz, se recolorea a negro al final para cumplir la regla.

  • Los punteros izquierdo y derecho apuntan al nodo NIL negro compartido.
  • Se guarda el puntero al padre si la estructura lo maneja.

9.3 Casos de recoloreo

Si el padre es rojo y el tío también es rojo, hay una violación de dos rojos consecutivos. La corrección es solo de colores:

  • Padre → negro.
  • Tío → negro.
  • Abuelo → rojo (salvo que sea la raíz; en ese caso queda negro).
  • Subir el puntero al abuelo y seguir verificando hacia arriba.

Este caso no requiere rotaciones y mantiene la altura negra en todos los caminos.

9.4 Casos de rotación

Si el padre es rojo y el tío es negro (o NIL), las rotaciones eliminan los rojos consecutivos. Se analizan dos formas:

  • Zig-zag (LR o RL): rotar primero al padre para convertir la forma en línea y luego rotar al abuelo.
  • Línea (LL o RR): rotar directamente al abuelo en sentido opuesto al sesgo.

Tras la rotación final, el nuevo padre de la subestructura se colorea negro y el abuelo original se colorea rojo para evitar rojos consecutivos y conservar la altura negra.

def arreglar_insercion(raiz_ref, nodo, nil):
  while nodo.padre != nil and nodo.padre.color == ROJO:
    p = nodo.padre
    g = p.padre
    padre_es_izq = (p == g.izquierdo)
    tio = g.derecho if padre_es_izq else g.izquierdo

    if tio.color == ROJO:
      # Caso tio rojo: solo recolorear
      p.color = NEGRO
      tio.color = NEGRO
      g.color = ROJO
      nodo = g
      continue

    # Tio negro: rotaciones
    if padre_es_izq and nodo == p.derecho:
      rotar_izquierda(p, raiz_ref)
      nodo = p
      p = nodo.padre
    elif not padre_es_izq and nodo == p.izquierdo:
      rotar_derecha(p, raiz_ref)
      nodo = p
      p = nodo.padre

    # Forma en linea
    p.color = NEGRO
    g.color = ROJO
    if padre_es_izq:
      rotar_derecha(g, raiz_ref)
    else:
      rotar_izquierda(g, raiz_ref)
  raiz_ref[0].color = NEGRO

def insertar_rbt(raiz, clave, nil):
  # 1) Insercion tipo BST
  padre = nil
  cur = raiz
  while cur != nil:
    padre = cur
    if clave < cur.clave:
      cur = cur.izquierdo
    elif clave > cur.clave:
      cur = cur.derecho
    else:
      return raiz  # duplicado

  nuevo = crear_nodo_rbt(clave, padre, nil)
  if padre == nil:
    raiz = nuevo
  elif clave < padre.clave:
    padre.izquierdo = nuevo
  else:
    padre.derecho = nuevo

  # 2) Arreglar colores/rotaciones
  raiz_ref = [raiz]
  arreglar_insercion(raiz_ref, nuevo, nil)
  return raiz_ref[0]

9.5 Código completo para probar en Python

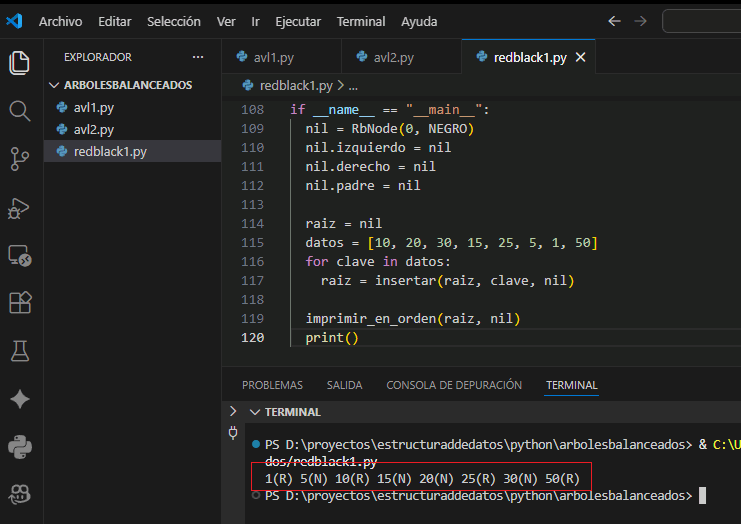
Ejemplo autocontenible con nodo NIL compartido, inserción y correcciones. Copia y ejecuta.

ROJO = "ROJO"
NEGRO = "NEGRO"

class RbNode:
  def __init__(self, clave, color=ROJO, padre=None, nil=None):
    self.clave = clave
    self.color = color
    self.izquierdo = nil
    self.derecho = nil
    self.padre = padre if padre else nil

def crear_nodo(clave, padre, nil):
  return RbNode(clave, ROJO, padre, nil)

def rotar_izquierda(raiz_ref, x, nil):
  y = x.derecho
  x.derecho = y.izquierdo
  if y.izquierdo != nil:
    y.izquierdo.padre = x
  y.padre = x.padre
  if x.padre == nil:
    raiz_ref[0] = y
  elif x == x.padre.izquierdo:
    x.padre.izquierdo = y
  else:
    x.padre.derecho = y
  y.izquierdo = x
  x.padre = y

def rotar_derecha(raiz_ref, y, nil):
  x = y.izquierdo
  y.izquierdo = x.derecho
  if x.derecho != nil:
    x.derecho.padre = y
  x.padre = y.padre
  if y.padre == nil:
    raiz_ref[0] = x
  elif y == y.padre.izquierdo:
    y.padre.izquierdo = x
  else:
    y.padre.derecho = x
  x.derecho = y
  y.padre = x

def arreglar_insercion(raiz_ref, n, nil):
  while n.padre != nil and n.padre.color == ROJO:
    p = n.padre
    g = p.padre
    padre_es_izq = (p == g.izquierdo)
    tio = g.derecho if padre_es_izq else g.izquierdo

    if tio.color == ROJO:
      p.color = NEGRO
      tio.color = NEGRO
      g.color = ROJO
      n = g
      continue

    if padre_es_izq and n == p.derecho:
      rotar_izquierda(raiz_ref, p, nil)
      n = p
      p = n.padre
    elif not padre_es_izq and n == p.izquierdo:
      rotar_derecha(raiz_ref, p, nil)
      n = p
      p = n.padre

    p.color = NEGRO
    g.color = ROJO
    if padre_es_izq:
      rotar_derecha(raiz_ref, g, nil)
    else:
      rotar_izquierda(raiz_ref, g, nil)
  raiz_ref[0].color = NEGRO

def insertar(raiz, clave, nil):
  padre = nil
  cur = raiz
  while cur != nil:
    padre = cur
    if clave < cur.clave:
      cur = cur.izquierdo
    elif clave > cur.clave:
      cur = cur.derecho
    else:
      return raiz

  nuevo = crear_nodo(clave, padre, nil)
  if padre == nil:
    raiz = nuevo
  elif clave < padre.clave:
    padre.izquierdo = nuevo
  else:
    padre.derecho = nuevo

  raiz_ref = [raiz]
  arreglar_insercion(raiz_ref, nuevo, nil)
  return raiz_ref[0]

def imprimir_en_orden(n, nil):
  if n == nil:
    return
  imprimir_en_orden(n.izquierdo, nil)
  color = "R" if n.color == ROJO else "N"
  print(f"{n.clave}({color})", end=" ")
  imprimir_en_orden(n.derecho, nil)

if __name__ == "__main__":
  nil = RbNode(0, NEGRO)
  nil.izquierdo = nil
  nil.derecho = nil
  nil.padre = nil

  raiz = nil
  datos = [10, 20, 30, 15, 25, 5, 1, 50]
  for clave in datos:
    raiz = insertar(raiz, clave, nil)

  imprimir_en_orden(raiz, nil)
  print()
Editor online
Secuencia de eliminación y rebalanceo en un árbol AVL
Retornar