Árboles en C - Árboles binarios de búsqueda

Un árbol binario de búsqueda (ABB o BST) organiza los datos de modo que cada nodo cumple la regla: los valores del subárbol izquierdo son menores que el valor del nodo y los del subárbol derecho son mayores o iguales. Esto permite localizar elementos en tiempo logarítmico cuando el árbol está balanceado y facilita algoritmos de ordenación y filtrado.

6.1 Estructura y utilidades básicas

Utilizamos el mismo modelo de nodo presentado en los temas anteriores, lo que nos permite compartir funciones de inserción y recorridos sin modificaciones.

typedef struct TreeNode {
  int valor;
  struct TreeNode *izquierdo;
  struct TreeNode *derecho;
  unsigned char nivel;
} TreeNode;

typedef struct {
  TreeNode *raiz;
  unsigned int cantidad;
} ArbolBusqueda;

6.2 Inserción iterativa

La inserción sigue el mismo patrón que en el tema 3: avanzamos según la comparación y colocamos el nodo en el primer puntero nulo.

TreeNode *insertarABB(ArbolBusqueda *arbol, int valor) {
  if (!arbol->raiz) {
    TreeNode *nodo = crearNodo(valor);
    if (!nodo) return NULL;
    arbol->raiz = nodo;
    arbol->cantidad = 1;
    return nodo;
  }

  TreeNode *actual = arbol->raiz;
  TreeNode *anterior = NULL;
  while (actual) {
    anterior = actual;
    if (valor < actual->valor) {
      actual = actual->izquierdo;
    } else {
      actual = actual->derecho;
    }
  }

  TreeNode *nuevo = crearNodo(valor);
  if (!nuevo) return NULL;
  nuevo->nivel = (unsigned char)(anterior->nivel + 1);
  if (valor < anterior->valor) {
    anterior->izquierdo = nuevo;
  } else {
    anterior->derecho = nuevo;
  }
  arbol->cantidad++;
  return nuevo;
}

6.3 Búsqueda

Encontrar un valor aprovecha la misma regla. Si el valor buscado es menor que el nodo actual, exploramos el subárbol izquierdo; de lo contrario, el derecho.

TreeNode *buscarABB(TreeNode *nodo, int valor) {
  while (nodo) {
    if (valor == nodo->valor) {
      return nodo;
    }
    if (valor < nodo->valor) {
      nodo = nodo->izquierdo;
    } else {
      nodo = nodo->derecho;
    }
  }
  return NULL;
}

6.4 Valor mínimo y máximo

El mínimo se obtiene siguiendo la rama izquierda hasta encontrar una hoja. El máximo aplica el mismo principio hacia la derecha.

TreeNode *minimo(TreeNode *nodo) {
  if (!nodo) return NULL;
  while (nodo->izquierdo) {
    nodo = nodo->izquierdo;
  }
  return nodo;
}

TreeNode *maximo(TreeNode *nodo) {
  if (!nodo) return NULL;
  while (nodo->derecho) {
    nodo = nodo->derecho;
  }
  return nodo;
}

6.5 Eliminación

Eliminar un nodo requiere manejar tres casos clásicos:

Hoja: se elimina directamente.
Un solo hijo: se conecta el hijo con el padre y se libera el nodo.
Dos hijos: se reemplaza con el sucesor (mínimo del subárbol derecho) o el predecesor.

TreeNode *eliminarABB(TreeNode *raiz, int valor) {
  if (!raiz) return NULL;

  if (valor < raiz->valor) {
    raiz->izquierdo = eliminarABB(raiz->izquierdo, valor);
  } else if (valor > raiz->valor) {
    raiz->derecho = eliminarABB(raiz->derecho, valor);
  } else {
    if (!raiz->izquierdo) {
      TreeNode *derecho = raiz->derecho;
      free(raiz);
      return derecho;
    }
    if (!raiz->derecho) {
      TreeNode *izquierdo = raiz->izquierdo;
      free(raiz);
      return izquierdo;
    }
    TreeNode *sucesor = minimo(raiz->derecho);
    raiz->valor = sucesor->valor;
    raiz->derecho = eliminarABB(raiz->derecho, sucesor->valor);
  }
  return raiz;
}

6.6 Verificar la propiedad de ABB

Cuando el código proviene de fuentes externas conviene validar que el árbol respete la regla de ordenamiento. Esto se logra comprobando rangos permitidos en cada nodo.

int esABB(TreeNode *nodo, int min, int max) {
  if (!nodo) return 1;
  if (nodo->valor < min || nodo->valor > max) return 0;
  return esABB(nodo->izquierdo, min, nodo->valor - 1) &&
         esABB(nodo->derecho, nodo->valor + 1, max);
}

6.7 Consideraciones de equilibrio

Un ABB puede degradarse a una lista cuando los datos llegan casi ordenados. Para mitigar el problema:

Barajar la entrada antes de insertar.
Rebalancear periódicamente usando el recorrido inorden.
Adoptar variantes auto-balanceadas (AVL, Red-Black) si la carga de trabajo lo exige.

6.8 Código completo para CLion

El siguiente programa integra inserción, búsqueda, obtención de extremos y eliminación en un ABB.

#include <stdio.h>
#include <stdlib.h>

typedef struct TreeNode {
  int valor;
  struct TreeNode *izquierdo;
  struct TreeNode *derecho;
} TreeNode;

typedef struct {
  TreeNode *raiz;
  unsigned int cantidad;
} ArbolBusqueda;

TreeNode *crearNodo(int valor) {
  TreeNode *nodo = malloc(sizeof(TreeNode));
  if (!nodo) return NULL;
  nodo->valor = valor;
  nodo->izquierdo = NULL;
  nodo->derecho = NULL;
  return nodo;
}

TreeNode *insertarABB(ArbolBusqueda *arbol, int valor) {
  if (!arbol->raiz) {
    TreeNode *nodo = crearNodo(valor);
    if (!nodo) return NULL;
    arbol->raiz = nodo;
    arbol->cantidad = 1;
    return nodo;
  }
  TreeNode *actual = arbol->raiz;
  TreeNode *anterior = NULL;
  while (actual) {
    anterior = actual;
    if (valor < actual->valor) actual = actual->izquierdo;
    else actual = actual->derecho;
  }
  TreeNode *nuevo = crearNodo(valor);
  if (!nuevo) return NULL;
  if (valor < anterior->valor) anterior->izquierdo = nuevo;
  else anterior->derecho = nuevo;
  arbol->cantidad++;
  return nuevo;
}

TreeNode *buscarABB(TreeNode *nodo, int valor) {
  while (nodo) {
    if (valor == nodo->valor) return nodo;
    nodo = (valor < nodo->valor) ? nodo->izquierdo : nodo->derecho;
  }
  return NULL;
}

TreeNode *minimo(TreeNode *nodo) {
  if (!nodo) return NULL;
  while (nodo->izquierdo) nodo = nodo->izquierdo;
  return nodo;
}

TreeNode *eliminarABB(TreeNode *raiz, int valor) {
  if (!raiz) return NULL;
  if (valor < raiz->valor) {
    raiz->izquierdo = eliminarABB(raiz->izquierdo, valor);
  } else if (valor > raiz->valor) {
    raiz->derecho = eliminarABB(raiz->derecho, valor);
  } else {
    if (!raiz->izquierdo) {
      TreeNode *derecho = raiz->derecho;
      free(raiz);
      return derecho;
    }
    if (!raiz->derecho) {
      TreeNode *izquierdo = raiz->izquierdo;
      free(raiz);
      return izquierdo;
    }
    TreeNode *sucesor = minimo(raiz->derecho);
    raiz->valor = sucesor->valor;
    raiz->derecho = eliminarABB(raiz->derecho, sucesor->valor);
  }
  return raiz;
}

void imprimirInorden(TreeNode *nodo) {
  if (!nodo) return;
  imprimirInorden(nodo->izquierdo);
  printf("%d ", nodo->valor);
  imprimirInorden(nodo->derecho);
}

void liberarArbol(TreeNode *nodo) {
  if (!nodo) return;
  liberarArbol(nodo->izquierdo);
  liberarArbol(nodo->derecho);
  free(nodo);
}

int main(void) {
  ArbolBusqueda abb = {0};
  int valores[] = {15, 8, 20, 4, 10, 17, 25};
  unsigned int total = (unsigned int)(sizeof(valores)/sizeof(valores[0]));
  for (unsigned int i = 0; i < total; i++) {
    insertarABB(&abb, valores[i]);
  }

  puts("Inorden:");
  imprimirInorden(abb.raiz);

  int objetivo = 10;
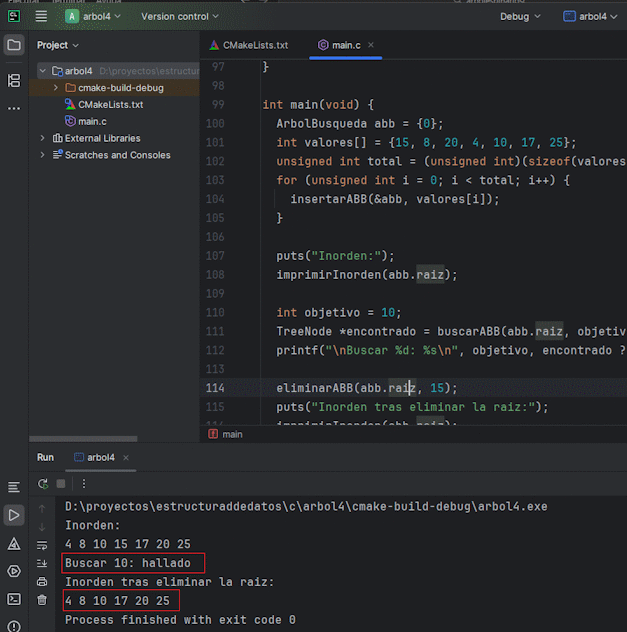
  TreeNode *encontrado = buscarABB(abb.raiz, objetivo);
  printf("\nBuscar %d: %s\n", objetivo, encontrado ? "hallado" : "no encontrado");

  eliminarABB(abb.raiz, 15);
  puts("Inorden tras eliminar la raiz:");
  imprimirInorden(abb.raiz);

  liberarArbol(abb.raiz);
  return 0;
}

Representación de un árbol binario de búsqueda

Retornar

6 - Árboles binarios de búsqueda