6 - Eliminación en un árbol B
Eliminar en un B-Tree debe preservar los invariantes: cada nodo (salvo la raíz) mantiene entre t - 1 y 2t - 1 claves y las hojas permanecen en el mismo nivel. La estrategia top-down evita quedarse sin espacio al regresar de la recursión.
6.1 Eliminación de clave en nodo hoja
Si la clave está en una hoja con al menos t claves:
- Se elimina directamente desplazando las claves mayores para cerrar el hueco.
- No hay cambios en otros nodos porque la hoja sigue teniendo al menos
t - 1claves.
6.2 Eliminación en nodo interno
Cuando la clave está en un nodo interno:
- Si el hijo izquierdo tiene
≥ tclaves, se toma su predecesora (máxima del subárbol izquierdo) para reemplazar y se borra recursivamente allí. - Si el hijo derecho tiene
≥ tclaves, se toma la sucesora (mínima del subárbol derecho) y se elimina en ese hijo. - Si ambos hijos tienen solo
t - 1claves, se fusionan con la clave actual y se continua en el nodo fusionado.
6.3 Fusión (merge) de nodos
La fusión combina dos hijos hermanos con t - 1 claves cada uno y la clave separadora del padre:
- Se crean
2t - 1claves en un solo nodo y se unen sus hijos (si existen). - El padre pierde una clave y un puntero; si queda con menos de
t - 1claves se tratará más arriba. - Permite seguir la eliminación en un nodo con espacio suficiente.
6.4 Redistribución de claves entre hermanos
Antes de fusionar conviene redistribuir cuando un hermano tiene ≥ t claves:
- Si el hermano izquierdo está cargado, se mueve su mayor clave al padre y la clave del padre baja al nodo deficitario.
- Si el hermano derecho está cargado, se sube su menor clave y se baja la clave del padre.
- Con esto se evita fusionar y se mantiene la ocupación de ambos nodos.
6.5 Actualizar la raíz si queda vacía
Tras eliminar puede ocurrir que la raíz se quede sin claves:
- Si tiene un solo hijo, este pasa a ser la nueva raíz (reduce la altura en uno).
- Si no tiene hijos, el árbol queda vacío.
- Esta actualización mantiene la raíz con al menos una clave salvo en el caso del árbol vacío.
# Eliminacion top-down en B-Tree (bosquejo)
def btree_eliminar(raiz, clave):
if raiz is None:
return None
eliminar_en_nodo(raiz, clave)
# Si la raiz quedo sin claves, ajustarla
if raiz.cuenta == 0:
raiz = None if raiz.es_hoja else raiz.hijos[0]
return raiz
# eliminar_en_nodo garantiza que al descender el hijo elegido tenga >= t claves:
# - si un hijo tiene solo t-1, intenta redistribuir con un hermano
# - si ambos hermanos tienen t-1, fusiona y luego desciende
def eliminar_en_nodo(nodo, clave):
# Detalles omitidos por brevedad: casos de hoja, sustituci¢n por predecesor/sucesor,
# redistribucion y fusion segun ocupacion de hermanos.
pass6.6 Código completo para probar en VSCode
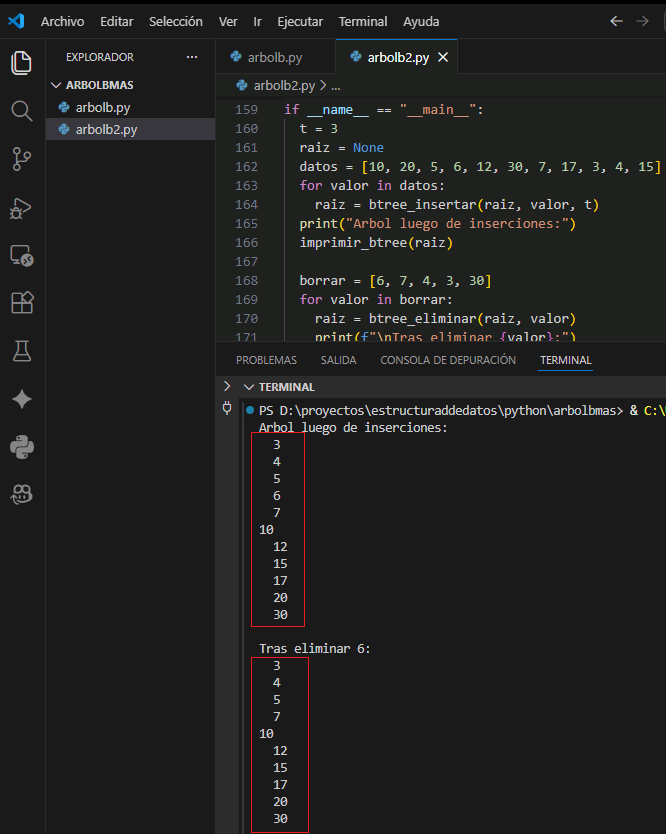
Ejemplo autocontenido en main.py con inserción y eliminación top-down listo para ejecutar:
class BTreeNode:
def __init__(self, orden, es_hoja):
self.claves = []
self.hijos = []
self.cuenta = 0
self.es_hoja = es_hoja
self.orden = orden
def dividir_hijo(padre, idx, hijo):
t = hijo.orden
nuevo = BTreeNode(t, hijo.es_hoja)
clave_media = hijo.claves[t - 1]
nuevo.claves = hijo.claves[t:]
if not hijo.es_hoja:
nuevo.hijos = hijo.hijos[t:]
hijo.claves = hijo.claves[:t - 1]
if not hijo.es_hoja:
hijo.hijos = hijo.hijos[:t]
hijo.cuenta = len(hijo.claves)
nuevo.cuenta = len(nuevo.claves)
padre.hijos.insert(idx + 1, nuevo)
padre.claves.insert(idx, clave_media)
padre.cuenta = len(padre.claves)
def insertar_no_lleno(nodo, clave):
i = nodo.cuenta - 1
if nodo.es_hoja:
nodo.claves.append(0)
while i >= 0 and clave < nodo.claves[i]:
nodo.claves[i + 1] = nodo.claves[i]
i -= 1
nodo.claves[i + 1] = clave
nodo.cuenta += 1
else:
while i >= 0 and clave < nodo.claves[i]:
i -= 1
i += 1
if nodo.hijos[i].cuenta == 2 * nodo.orden - 1:
dividir_hijo(nodo, i, nodo.hijos[i])
if clave > nodo.claves[i]:
i += 1
insertar_no_lleno(nodo.hijos[i], clave)
def btree_insertar(raiz, clave, orden):
if raiz is None:
raiz = BTreeNode(orden, True)
if raiz.cuenta == 2 * raiz.orden - 1:
nueva = BTreeNode(raiz.orden, False)
nueva.hijos.append(raiz)
dividir_hijo(nueva, 0, raiz)
raiz = nueva
insertar_no_lleno(raiz, clave)
return raiz
# ---------- Eliminacion ----------
def maximo(nodo):
while not nodo.es_hoja:
nodo = nodo.hijos[nodo.cuenta]
return nodo.claves[nodo.cuenta - 1]
def minimo(nodo):
while not nodo.es_hoja:
nodo = nodo.hijos[0]
return nodo.claves[0]
def fusionar(padre, idx):
t = padre.orden
izq = padre.hijos[idx]
der = padre.hijos[idx + 1]
izq.claves.insert(t - 1, padre.claves.pop(idx))
izq.claves.extend(der.claves)
if not izq.es_hoja:
izq.hijos.extend(der.hijos)
izq.cuenta = len(izq.claves)
padre.hijos.pop(idx + 1)
padre.cuenta = len(padre.claves)
def redistribuir_izq(padre, idx):
hijo = padre.hijos[idx]
hermano = padre.hijos[idx - 1]
hijo.claves.insert(0, padre.claves[idx - 1])
if not hijo.es_hoja:
hijo.hijos.insert(0, hermano.hijos.pop())
padre.claves[idx - 1] = hermano.claves.pop()
hermano.cuenta = len(hermano.claves)
hijo.cuenta = len(hijo.claves)
def redistribuir_der(padre, idx):
hijo = padre.hijos[idx]
hermano = padre.hijos[idx + 1]
hijo.claves.append(padre.claves[idx])
if not hijo.es_hoja:
hijo.hijos.append(hermano.hijos.pop(0))
padre.claves[idx] = hermano.claves.pop(0)
hermano.cuenta = len(hermano.claves)
hijo.cuenta = len(hijo.claves)
def asegurar_claves(padre, idx):
t = padre.orden
hijo = padre.hijos[idx]
if hijo.cuenta >= t:
return
if idx > 0 and padre.hijos[idx - 1].cuenta >= t:
redistribuir_izq(padre, idx)
elif idx < padre.cuenta and padre.hijos[idx + 1].cuenta >= t:
redistribuir_der(padre, idx)
else:
if idx < padre.cuenta:
fusionar(padre, idx)
else:
fusionar(padre, idx - 1)
def eliminar_en_nodo(nodo, clave):
idx = 0
while idx < nodo.cuenta and clave > nodo.claves[idx]:
idx += 1
if idx < nodo.cuenta and nodo.claves[idx] == clave:
if nodo.es_hoja:
nodo.claves.pop(idx)
nodo.cuenta -= 1
else:
if nodo.hijos[idx].cuenta >= nodo.orden:
pred = maximo(nodo.hijos[idx])
nodo.claves[idx] = pred
eliminar_en_nodo(nodo.hijos[idx], pred)
elif nodo.hijos[idx + 1].cuenta >= nodo.orden:
succ = minimo(nodo.hijos[idx + 1])
nodo.claves[idx] = succ
eliminar_en_nodo(nodo.hijos[idx + 1], succ)
else:
fusionar(nodo, idx)
eliminar_en_nodo(nodo.hijos[idx], clave)
else:
if nodo.es_hoja:
return
asegurar_claves(nodo, idx)
if idx > nodo.cuenta:
idx -= 1
eliminar_en_nodo(nodo.hijos[idx], clave)
def btree_eliminar(raiz, clave):
if raiz is None:
return None
eliminar_en_nodo(raiz, clave)
if raiz.cuenta == 0:
raiz = None if raiz.es_hoja else raiz.hijos[0]
return raiz
def imprimir_btree(nodo, nivel=0):
if nodo is None:
return
for i, clave in enumerate(nodo.claves):
if not nodo.es_hoja:
imprimir_btree(nodo.hijos[i], nivel + 1)
print(" " * nivel + str(clave))
if not nodo.es_hoja:
imprimir_btree(nodo.hijos[len(nodo.claves)], nivel + 1)
if __name__ == "__main__":
t = 3
raiz = None
datos = [10, 20, 5, 6, 12, 30, 7, 17, 3, 4, 15]
for valor in datos:
raiz = btree_insertar(raiz, valor, t)
print("Arbol luego de inserciones:")
imprimir_btree(raiz)
borrar = [6, 7, 4, 3, 30]
for valor in borrar:
raiz = btree_eliminar(raiz, valor)
print(f"\nTras eliminar {valor}:")
imprimir_btree(raiz)