14 - Árboles generados por recorridos

Al recorrer un grafo, cada vez que avanzamos a un nodo nuevo creamos una arista “de árbol”. Estas aristas forman un subgrafo sin ciclos que captura cómo alcanzamos cada vértice: el árbol de recorrido. Guardarlo permite reconstruir caminos, calcular niveles y clasificar el resto de las aristas.

14.1 Árbol BFS

El árbol BFS se genera tomando la primera vez que llegamos a cada nodo desde la cola. Sus propiedades clave:

  • Las aristas del árbol conectan nodos con niveles consecutivos (distancia mínima en aristas desde la raíz).
  • Cada nodo guarda su padre y su nivel; reconstruir el camino mínimo es retroceder por padres hasta la raíz.
  • En grafos no ponderados, el árbol BFS entrega las distancias mínimas en cantidad de aristas.

Abrir generador de árbol BFS

14.2 Árbol DFS

El árbol DFS se arma siguiendo aristas de árbol en el orden de profundización. Diferencias respecto de BFS:

  • La profundidad no representa distancia mínima, sino el orden en que se descendieron las llamadas recursivas.
  • Las aristas que no forman parte del árbol pueden ser de retroceso, avance o cruce; se detectan con tiempos de entrada/salida.
  • Es la base para detección de ciclos, orden topológico y Tarjan.

Abrir generador de árbol DFS

14.3 Vector padre[]

El vector padre[] guarda para cada vértice el nodo desde el cual fue descubierto. Se inicializa en -1 y se completa al marcar visitados. Usos típicos:

  • Reconstruir caminos y niveles sin volver a recorrer el grafo.
  • Construir explícitamente el árbol (lista de aristas padre-hijo).
  • Detectar ciclos en no dirigidos evitando contar la arista al padre.

14.4 Clasificación de aristas

Con los tiempos de descubrimiento (tin) y finalización (tout) del DFS podemos clasificar:

  • Tree edge: lleva a un nodo no visitado; forma parte del árbol DFS.
  • Back edge: apunta a un ancestro en la pila; indica ciclo.
  • Forward edge: va a un descendiente ya finalizado (solo en dirigidos).
  • Cross edge: conecta subárboles distintos o niveles sin relación directa.

14.5 Aplicaciones prácticas

  • Reconstruir rutas y distancias en navegación GPS o saltos mínimos de red usando el árbol BFS.
  • Encontrar ciclos, puentes y puntos de articulación a partir del árbol DFS y la clasificación de aristas.
  • Generar orden topológico y detectar dependencias imposibles en digrafos.
  • Reducir el grafo a su árbol de expansión para visualizaciones o simulaciones más livianas.

Implementación en C

Dos programas completos y separados para probar directamente en CLion. Ambos usan listas de adyacencia sin dependencias externas.

Arma el árbol BFS (programa completo)

#include <stdio.h>
#include <stdlib.h>

typedef struct Arista {
  int destino;
  struct Arista *sig;
} Arista;

typedef struct {
  int n;
  Arista **listas;
} Grafo;

Grafo crearGrafo(int n) {
  Grafo g;
  g.n = n;
  g.listas = calloc(n, sizeof(Arista *));
  return g;
}

void agregarAristaNoDirigida(Grafo *g, int u, int v) {
  Arista *a = malloc(sizeof(Arista));
  a->destino = v;
  a->sig = g->listas[u];
  g->listas[u] = a;

  Arista *b = malloc(sizeof(Arista));
  b->destino = u;
  b->sig = g->listas[v];
  g->listas[v] = b;
}

void imprimirArbolBFS(const Grafo *g, int origen) {
  int *padre = malloc(g->n * sizeof(int));
  int *nivel = malloc(g->n * sizeof(int));
  int *cola = malloc(g->n * sizeof(int));
  int ini = 0, fin = 0;

  for (int i = 0; i < g->n; i++) {
    padre[i] = -1;
    nivel[i] = -1;
  }
  padre[origen] = origen;
  nivel[origen] = 0;
  cola[fin++] = origen;

  printf("Arbol BFS (origen %d):\n", origen);
  while (ini < fin) {
    int u = cola[ini++];
    for (Arista *it = g->listas[u]; it; it = it->sig) {
      int v = it->destino;
      if (padre[v] == -1) {
        padre[v] = u;
        nivel[v] = nivel[u] + 1;
        printf("%d -- %d (nivel %d)\n", u, v, nivel[v]);
        cola[fin++] = v;
      }
    }
  }

  free(padre);
  free(nivel);
  free(cola);
}

int main(void) {
  Grafo g = crearGrafo(6);
  agregarAristaNoDirigida(&g, 0, 1);
  agregarAristaNoDirigida(&g, 0, 2);
  agregarAristaNoDirigida(&g, 1, 3);
  agregarAristaNoDirigida(&g, 1, 4);
  agregarAristaNoDirigida(&g, 2, 5);

          imprimirArbolBFS(&g, 0);
  return 0;
}

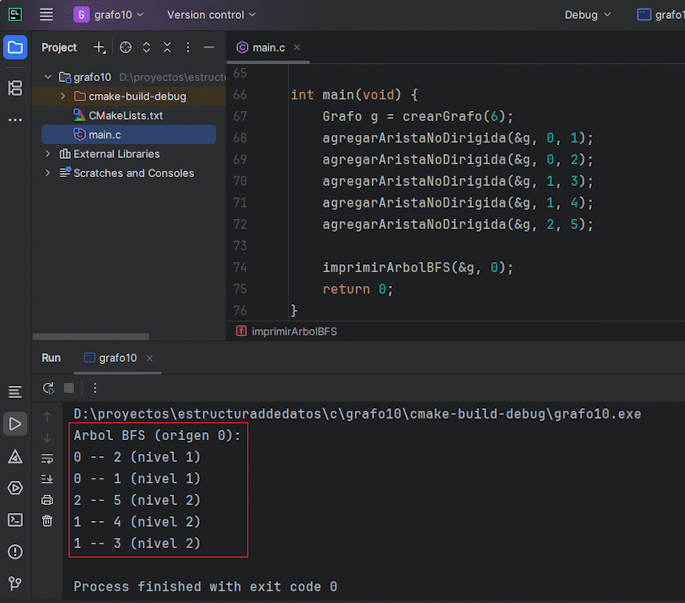
Ejemplo de recorrido y arbol DFS

Ejemplo de arbol DFS

Arma el árbol DFS (programa completo)

#include <stdio.h>
#include <stdlib.h>

typedef struct Arista {
  int destino;
  struct Arista *sig;
} Arista;

typedef struct {
  int n;
  Arista **listas;
} Grafo;

Grafo crearGrafo(int n) {
  Grafo g;
  g.n = n;
  g.listas = calloc(n, sizeof(Arista *));
  return g;
}

void agregarAristaNoDirigida(Grafo *g, int u, int v) {
  Arista *a = malloc(sizeof(Arista));
  a->destino = v;
  a->sig = g->listas[u];
  g->listas[u] = a;

  Arista *b = malloc(sizeof(Arista));
  b->destino = u;
  b->sig = g->listas[v];
  g->listas[v] = b;
}

void dfsArbol(const Grafo *g, int u, int padre, int nivel, int *visitado) {
  visitado[u] = 1;
  if (padre != -1) {
    printf("%d -- %d (nivel %d)\n", padre, u, nivel);
  }
  for (Arista *it = g->listas[u]; it; it = it->sig) {
    int v = it->destino;
    if (!visitado[v]) {
      dfsArbol(g, v, u, nivel + 1, visitado);
    }
  }
}

int main(void) {
  Grafo g = crearGrafo(6);
  agregarAristaNoDirigida(&g, 0, 1);
  agregarAristaNoDirigida(&g, 0, 2);
  agregarAristaNoDirigida(&g, 1, 3);
  agregarAristaNoDirigida(&g, 1, 4);
  agregarAristaNoDirigida(&g, 2, 5);

  int *visitado = calloc(g.n, sizeof(int));
  printf("Arbol DFS (origen %d):\n", 0);
  dfsArbol(&g, 0, -1, 0, visitado);
  free(visitado);
  return 0;
}

Comparativa de arboles de recorrido

Recorrido y arbol combinado

Retornar