15 - Detección de puentes (Bridges)

Un puente (o bridge) es una arista que, al eliminarla, incrementa la cantidad de componentes conexas de un grafo no dirigido. Identificarlos permite conocer puntos críticos de conectividad.

15.1 Concepto

• Solo aplica a grafos no dirigidos; en digrafos se requiere otra definición.
• Una arista u -- v es puente si no existe ningún camino alternativo entre u y v sin usar esa arista.
• En un árbol, todas las aristas son puentes; en un ciclo simple ninguna lo es.

15.2 Algoritmo de Tarjan

El algoritmo de Tarjan usa DFS con tiempos de descubrimiento tin y valores low que representan el tiempo mínimo alcanzable por back-edges.

• Inicializamos timer = 0; al entrar a un nodo u, asignamos tin[u] = low[u] = timer y luego incrementamos.
• Para cada vecino v: si es el padre en el árbol, se ignora; si no está visitado, se desciende y se actualiza low[u] = min(low[u], low[v]).
• Después de procesar un hijo v, la arista u -- v es puente si low[v] > tin[u].
• Si v ya estaba visitado (back-edge), actualizamos low[u] = min(low[u], tin[v]).

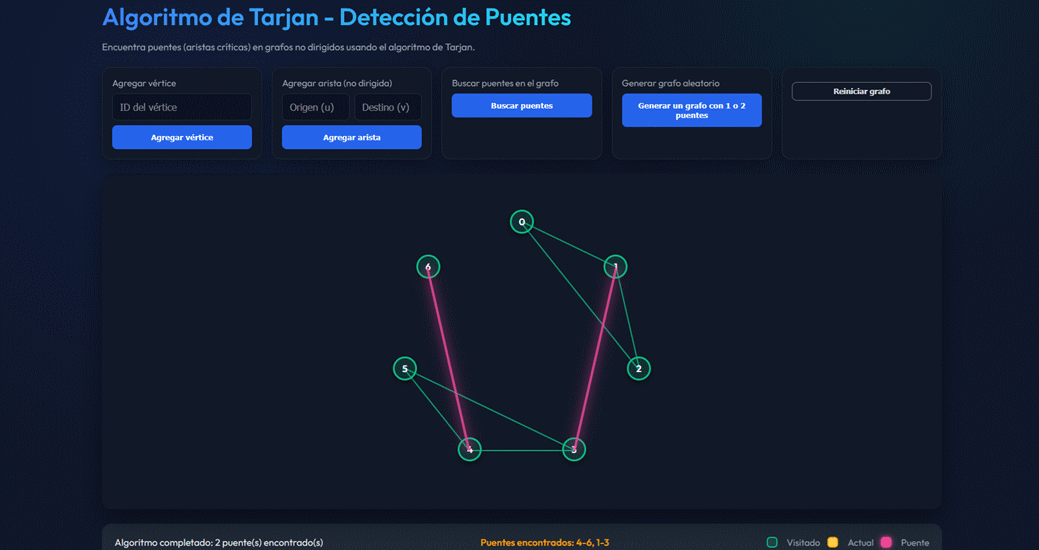
Simulador de detección de puentes

15.3 Aplicaciones

La detección de puentes es esencial en:

• Redes de comunicación: enlaces cuya caída rompe la red (routers, switches, cables submarinos, enlaces WiFi críticos).
• Ingeniería de software: en análisis de dependencias, módulos enlazados de forma crítica que aislan al sistema si fallan.
• Análisis de caminos alternativos: en mapas y rutas, puentes reales, túneles o calles sin alternativa.
• Detener propagación de fallas: en sistemas distribuidos, identificar enlaces vulnerables y mejorar la tolerancia a fallos.
• Grafos sociales: detectar vínculos débiles que conectan comunidades y puntos de separación entre grupos.

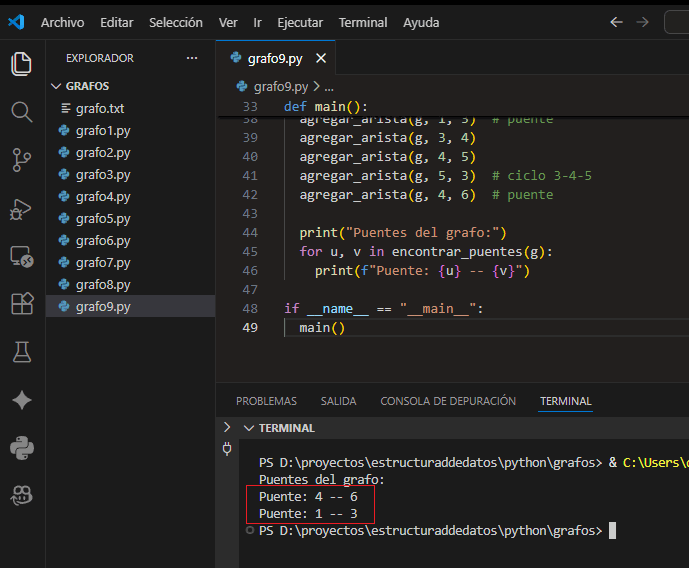
15.4 Aplicación completa para probar en VSCode

Implementación de Tarjan sobre lista de adyacencia. Imprime todas las aristas puente encontradas.

def agregar_arista(g, u, v):
  g[u].append((v, 1))
  g[v].append((u, 1))

def dfs_puentes(g, u, padre, visitado, tin, low, timer, puentes):
  visitado[u] = True
  tin[u] = low[u] = timer[0]
  timer[0] += 1

  for v, _ in g[u]:
    if v == padre:
      continue
    if not visitado[v]:
      dfs_puentes(g, v, u, visitado, tin, low, timer, puentes)
      if low[v] > tin[u]:
        puentes.append((u, v))
      low[u] = min(low[u], low[v])
    else:
      low[u] = min(low[u], tin[v])

def encontrar_puentes(g):
  visitado = {v: False for v in g}
  tin = {v: -1 for v in g}
  low = {v: -1 for v in g}
  timer = [0]
  puentes = []

  for u in g:
    if not visitado[u]:
      dfs_puentes(g, u, None, visitado, tin, low, timer, puentes)
  return puentes

def main():
  g = {i: [] for i in range(7)}
  agregar_arista(g, 0, 1)
  agregar_arista(g, 1, 2)
  agregar_arista(g, 2, 0)
  agregar_arista(g, 1, 3)  # puente
  agregar_arista(g, 3, 4)
  agregar_arista(g, 4, 5)
  agregar_arista(g, 5, 3)  # ciclo 3-4-5
  agregar_arista(g, 4, 6)  # puente

  print("Puentes del grafo:")
  for u, v in encontrar_puentes(g):
    print(f"Puente: {u} -- {v}")

if __name__ == "__main__":
  main()