16 - Puntos de articulación (Articulation Points)

Un punto de articulación es un vértice que, al eliminarlo junto con sus aristas incidentes, incrementa la cantidad de componentes conexas del grafo no dirigido. Detectarlos revela nodos críticos de conectividad.

16.1 Definición

• En un árbol, todos los nodos internos son puntos de articulación; las hojas no.
• En un ciclo simple, ningún nodo es punto de articulación.
• Solo consideramos grafos no dirigidos; en digrafos se requieren otras variantes.

16.2 Tarjan paso a paso

El algoritmo de Tarjan para puntos de articulación reutiliza tin y low con DFS:

• Asignamos tin[u] = low[u] = timer al descubrir u y luego incrementamos.
• Para cada vecino v: si es el padre, se ignora; si no está visitado, se desciende y luego low[u] = min(low[u], low[v]).
• Condición de articulación: si low[v] >= tin[u], el nodo u separa el subárbol de v del resto.
• La raíz del DFS es punto de articulación solo si tiene 2 o más hijos en el árbol DFS.

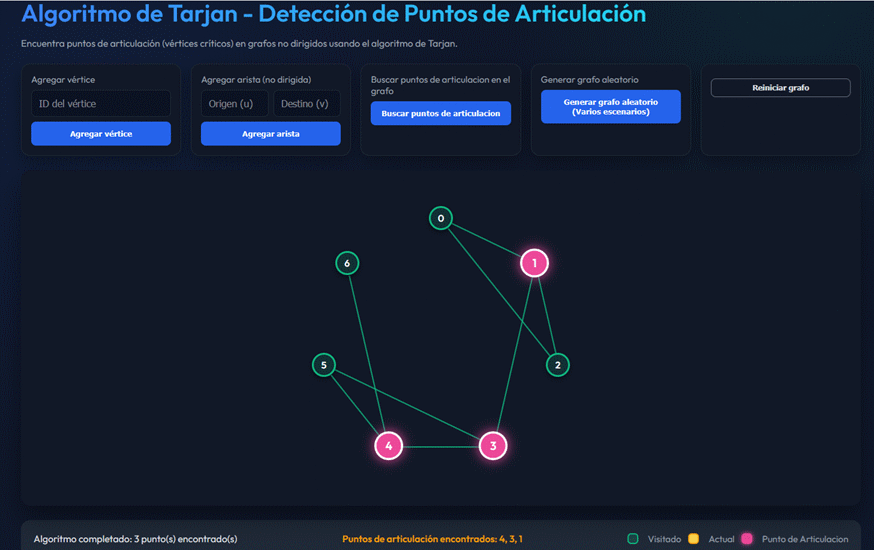
Simulador de puntos de articulación

16.3 Interpretación de resultados

• Un punto de articulación indica un nodo sin redundancia: su falla fragmenta la red.
• Al remover todos los puntos de articulación se obtiene un conjunto de componentes biconexas (bloques 2-conexos).
• Si no hay puntos de articulación, el grafo es 2-conexo respecto de vértices (no se separa al quitar un solo nodo).

16.4 Casos clave de conectividad

1. Nodos críticos de conectividad
   • Cada uno representa un punto central cuya eliminación separa el grafo en más componentes.
   • En una red de computadoras: routers centrales, switches clave, nodos que si fallan cortan la red.
2. Análisis de vulnerabilidad
   • En infraestructuras (red eléctrica, transporte): señalan dónde conviene redundar recursos.
   • Ejemplos: estaciones centrales, cruces críticos de rutas, subestaciones clave.
3. Detección de hubs en grafos sociales
   • Un nodo articulación puede ser la persona o entidad que conecta grupos distintos.
   • Si se retira, la red se fragmenta en comunidades separadas.

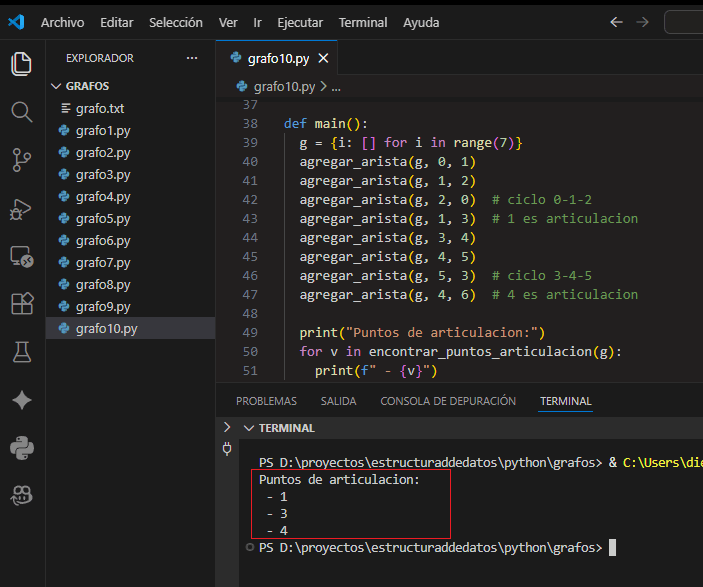
16.5 Aplicación completa para probar en VSCode

Implementación con listas de adyacencia que imprime todos los puntos de articulación encontrados.

def agregar_arista(g, u, v):
  g[u].append((v, 1))
  g[v].append((u, 1))

def dfs_articulacion(g, u, padre, visitado, tin, low, timer, es_articulacion):
  visitado[u] = True
  tin[u] = low[u] = timer[0]
  timer[0] += 1
  hijos = 0

  for v, _ in g[u]:
    if v == padre:
      continue
    if not visitado[v]:
      hijos += 1
      dfs_articulacion(g, v, u, visitado, tin, low, timer, es_articulacion)
      low[u] = min(low[u], low[v])
      if padre is not None and low[v] >= tin[u]:
        es_articulacion[u] = True
    else:
      low[u] = min(low[u], tin[v])

  if padre is None and hijos >= 2:
    es_articulacion[u] = True

def encontrar_puntos_articulacion(g):
  visitado = {v: False for v in g}
  tin = {v: -1 for v in g}
  low = {v: -1 for v in g}
  es_articulacion = {v: False for v in g}
  timer = [0]

  for u in g:
    if not visitado[u]:
      dfs_articulacion(g, u, None, visitado, tin, low, timer, es_articulacion)
  return [v for v, es in es_articulacion.items() if es]

def main():
  g = {i: [] for i in range(7)}
  agregar_arista(g, 0, 1)
  agregar_arista(g, 1, 2)
  agregar_arista(g, 2, 0)  # ciclo 0-1-2
  agregar_arista(g, 1, 3)  # 1 es articulacion
  agregar_arista(g, 3, 4)
  agregar_arista(g, 4, 5)
  agregar_arista(g, 5, 3)  # ciclo 3-4-5
  agregar_arista(g, 4, 6)  # 4 es articulacion

  print("Puntos de articulacion:")
  for v in encontrar_puntos_articulacion(g):
    print(f" - {v}")

if __name__ == "__main__":
  main()