18 - Caminos mínimos en grafos no ponderados
En un grafo no ponderado todas las aristas cuestan lo mismo: un paso. El camino mínimo entre dos vértices es el que usa la menor cantidad de aristas. Para este caso, el algoritmo ideal es la BFS (Breadth-First Search).
Simulador de camino mínimo en un grafo
18.1 BFS como Dijkstra sin peso
Cuando todos los pesos valen 1, no hace falta Dijkstra: BFS recorre por niveles y alcanza primero las distancias mínimas (Dijkstra se verá más adelante para grafos ponderados).
- Visita todos los vértices a distancia 1, luego a distancia 2, y así sucesivamente.
- La primera vez que llega a un nodo es por el camino más corto (en aristas).
Ejemplo: grafo A → B → C → D. Niveles: A (0), B (1), C (2), D (3). Distancia mínima A-D = 3 aristas. Camino: A → B → C → D.
18.2 Distancias mínimas
Se usa un arreglo dist inicializado en -1 y dist[origen] = 0. Al descubrir un vecino v desde u:
dist[v] = dist[u] + 1
Así se generan automáticamente las distancias en saltos.
18.3 Reconstrucción del camino
Para obtener el camino exacto se guarda padre (o prev): al descubrir v desde u, asignamos padre[v] = u. Luego:
camino = []
v = destino
mientras v != None:
camino.push(v)
v = padre[v]
invertir(camino)Ejemplo: padre[D]=C, padre[C]=B, padre[B]=A, padre[A]=None. Camino reconstruido: A → B → C → D.
18.4 Casos típicos
- Laberintos en grillas: cada casilla vale un movimiento; BFS encuentra la salida más corta. Probar demo
- Redes sociales: distancia mínima entre personas (grado de separación). Probar demo
- Juegos tipo Pac-Man sin pesos: cuando todas las celdas libres valen 1 movimiento, BFS permite que enemigos encuentren rutas cortas. Probar demo
- Movimientos de piezas de ajedrez: hallar el camino mínimo (por ejemplo un caballo) desde una casilla de origen hasta otra. Probar demo
- Transporte sin pesos: mínimo de estaciones, transbordos o calles.
- Redes de routers uniformes: cantidad de saltos entre nodos.
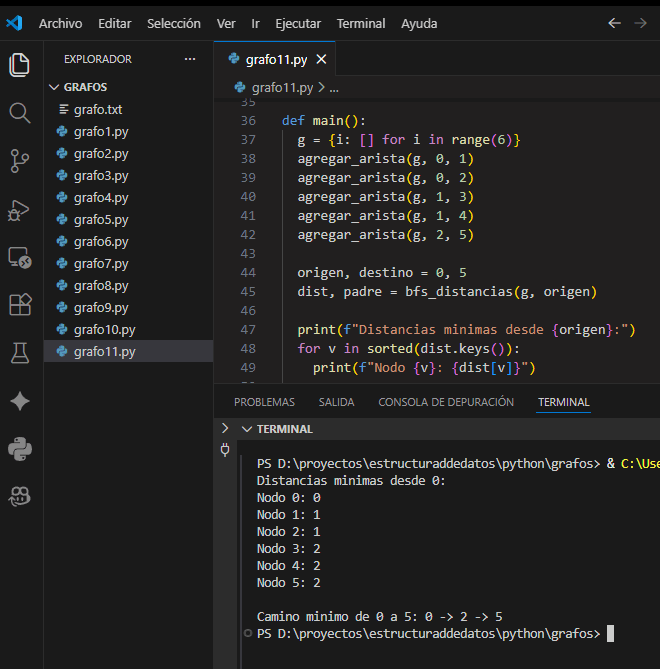
18.5 Algoritmo de caminos mínimos en grafos no ponderados (VSCode)
Implementación de BFS con distancias y reconstrucción del camino usando padre, con un grafo cargado en código (sin entrada por teclado).
from collections import deque
def agregar_arista(g, u, v):
g[u].append((v, 1))
g[v].append((u, 1))
def bfs_distancias(g, origen):
dist = {v: -1 for v in g}
padre = {v: None for v in g}
cola = deque([origen])
dist[origen] = 0
padre[origen] = origen
while cola:
u = cola.popleft()
for v, _ in g[u]:
if dist[v] == -1:
dist[v] = dist[u] + 1
padre[v] = u
cola.append(v)
return dist, padre
def reconstruir_camino(padre, origen, destino):
camino = []
v = destino
while v is not None:
camino.append(v)
if v == origen:
break
v = padre[v]
if not camino or camino[-1] != origen:
return None
camino.reverse()
return camino
def main():
g = {i: [] for i in range(6)}
agregar_arista(g, 0, 1)
agregar_arista(g, 0, 2)
agregar_arista(g, 1, 3)
agregar_arista(g, 1, 4)
agregar_arista(g, 2, 5)
origen, destino = 0, 5
dist, padre = bfs_distancias(g, origen)
print(f"Distancias minimas desde {origen}:")
for v in sorted(dist.keys()):
print(f"Nodo {v}: {dist[v]}")
print(f"\nCamino minimo de {origen} a {destino}: ", end="")
camino = reconstruir_camino(padre, origen, destino)
if camino is None:
print("no existe")
else:
print(" -> ".join(map(str, camino)))
if __name__ == "__main__":
main()