19 - Caminos mínimos en grafos ponderados (Dijkstra)

En muchos problemas reales (rutas, redes, mapas, costos) cada arista tiene un peso distinto. Buscamos el camino de costo mínimo, no solo menos saltos. Con pesos no negativos, el algoritmo clásico es Dijkstra.

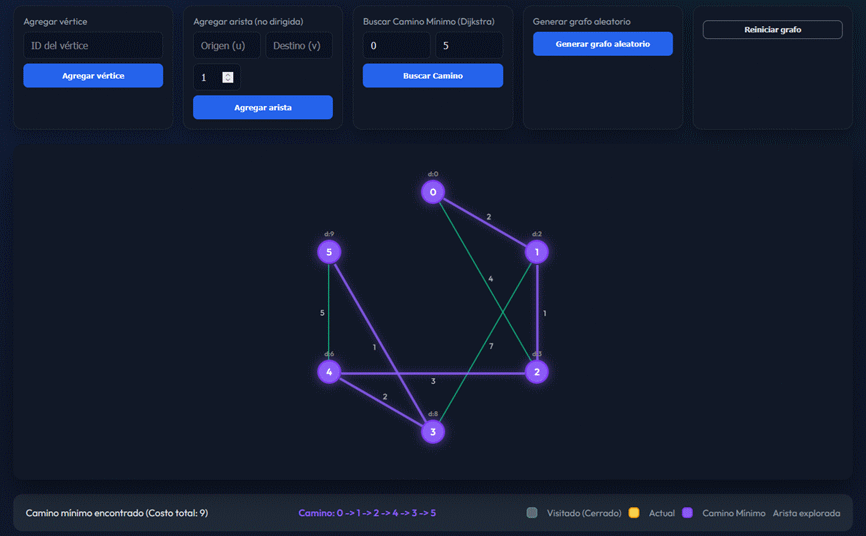
Simulador de camino mínimo en un grafo ponderado con Dijkstra

19.1 Idea general y cuándo usar Dijkstra

Problema: dado un grafo ponderado con pesos ≥ 0 y un origen s, hallar el costo mínimo desde s a todos los nodos.

• Ciudades unidas por rutas (peso = distancia).
• Routers conectados (peso = latencia).
• Tareas con dependencias (peso = tiempo de ejecución).

Dijkstra expande una frontera de nodos con distancia definitiva y relaja aristas hacia sus vecinos.

19.2 Conceptos clave del algoritmo

• dist[v]: mejor costo conocido desde s a v; inicia en infinito excepto dist[s]=0.
• visitado[v]: marca si la distancia ya es definitiva.
• padre[v]: anterior en el camino mínimo para reconstruir la ruta.

Relajación de v → u con peso w: si dist[v] + w < dist[u], entonces actualizar dist[u] y padre[u]=v.

19.3 Dijkstra paso a paso (versión simple, sin heap)

1. Inicializar dist[*]=INF, visitado[*]=False; dist[s]=0.
2. Repetir n veces: elegir el no visitado con dist mínima; si es None o infinito, terminar.
3. Marcarlo como visitado y relajar sus aristas.

Al final, dist[v] tiene el costo mínimo y padre[v] permite reconstruir el camino. Condición: todos los pesos deben ser ≥ 0; con negativos usar Bellman-Ford.

19.4 Usos típicos de Dijkstra

• GPS y mapas: peso = km o tiempo estimado.
• Redes de computadoras: peso = latencia; protocolos como OSPF lo usan.
• Logística: minimizar costo de envío entre depósito y cliente.
• Videojuegos / IA: peso = dificultad del terreno.
• Planificación de tareas: peso = tiempo; en DAG da el tiempo total mínimo respetando dependencias.

19.5 Implementación con listas de adyacencia (sin heap)

Usamos listas de adyacencia con pares (destino, peso) y selección lineal del mínimo.

def agregar_arista_dirigida(g, u, v, w):
  g[u].append((v, w))

19.6 Aplicación completa para probar en VSCode

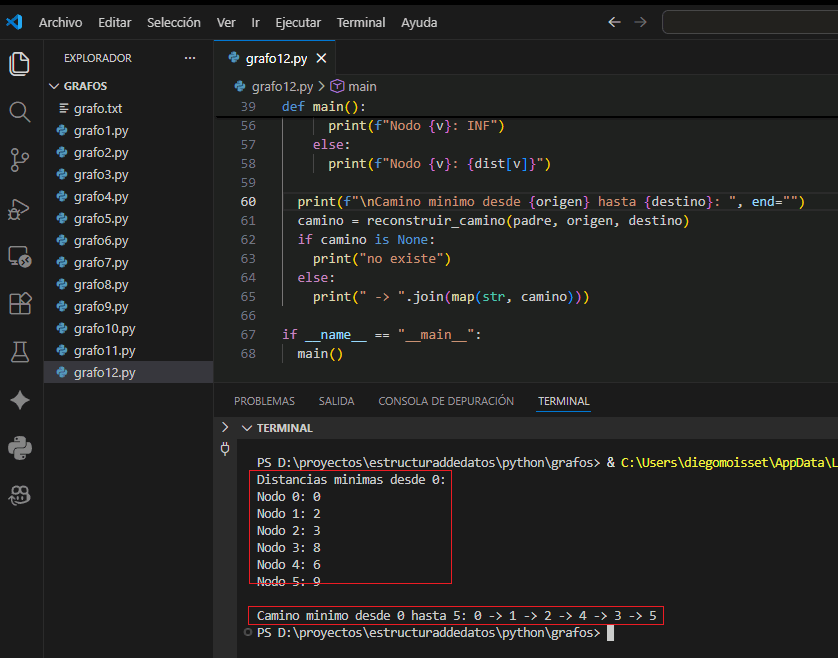
Programa completo: usa un grafo cargado en código (sin entrada por teclado), ejecuta Dijkstra desde un origen fijo, muestra distancias y reconstruye un camino.

INF = 10**9

def agregar_arista_dirigida(g, u, v, w):
  g[u].append((v, w))

def dijkstra(g, origen):
  dist = {v: INF for v in g}
  padre = {v: None for v in g}
  visitado = {v: False for v in g}
  dist[origen] = 0

  for _ in range(len(g)):
    v_min = None
    for v in g:
      if not visitado[v] and (v_min is None or dist[v] < dist[v_min]):
        v_min = v
    if v_min is None or dist[v_min] == INF:
      break
    visitado[v_min] = True
    for u, w in g[v_min]:
      if dist[v_min] + w < dist[u]:
        dist[u] = dist[v_min] + w
        padre[u] = v_min
  return dist, padre

def reconstruir_camino(padre, origen, destino):
  camino = []
  v = destino
  while v is not None:
    camino.append(v)
    if v == origen:
      break
    v = padre[v]
  if not camino or camino[-1] != origen:
    return None
  camino.reverse()
  return camino

def main():
  g = {i: [] for i in range(6)}
  agregar_arista_dirigida(g, 0, 1, 2)
  agregar_arista_dirigida(g, 0, 2, 4)
  agregar_arista_dirigida(g, 1, 2, 1)
  agregar_arista_dirigida(g, 1, 3, 7)
  agregar_arista_dirigida(g, 2, 4, 3)
  agregar_arista_dirigida(g, 4, 3, 2)
  agregar_arista_dirigida(g, 3, 5, 1)
  agregar_arista_dirigida(g, 4, 5, 5)

  origen, destino = 0, 5
  dist, padre = dijkstra(g, origen)

  print(f"Distancias minimas desde {origen}:")
  for v in sorted(dist.keys()):
    if dist[v] == INF:
      print(f"Nodo {v}: INF")
    else:
      print(f"Nodo {v}: {dist[v]}")

  print(f"\nCamino minimo desde {origen} hasta {destino}: ", end="")
  camino = reconstruir_camino(padre, origen, destino)
  if camino is None:
    print("no existe")
  else:
    print(" -> ".join(map(str, camino)))

if __name__ == "__main__":
  main()