4 - Matriz de adyacencia en Python
La matriz de adyacencia ofrece consultas O(1) para saber si dos vértices están conectados. En este tema construimos una versión modular en Python y cubrimos desde la estructura base hasta operaciones de inserción, eliminación, verificación e impresión.
4.1 Estructura base
Definimos un contenedor que guarde el tamaño y la matriz.
class MatrizAdy:
def __init__(self, n):
self.n = n
self.m = [[0 for _ in range(n)] for _ in range(n)]4.2 Declaración y creación dinámica
Construimos la matriz en memoria, inicializando en 0 (sin aristas).
def crear_matriz(n):
if n <= 0:
return None
return MatrizAdy(n)4.3 Insertar aristas
Asignamos un valor distinto de 0 para marcar la existencia de una arista o su peso. Para grafos no dirigidos, se escribe en ambas posiciones.
def insertar_arista(g, u, v, peso=1, es_dirigido=False):
if g is None or not (0 <= u < g.n and 0 <= v < g.n):
return
g.m[u][v] = peso if peso != 0 else 1
if not es_dirigido:
g.m[v][u] = g.m[u][v]4.4 Eliminar aristas
Revertimos el valor a 0 para indicar ausencia de conexión.
def eliminar_arista(g, u, v, es_dirigido=False):
if g is None or not (0 <= u < g.n and 0 <= v < g.n):
return
g.m[u][v] = 0
if not es_dirigido:
g.m[v][u] = 04.5 Verificar adyacencia
Comprobamos si el valor almacenado es distinto de 0. En grafos ponderados, el valor es el peso.
def son_adyacentes(g, u, v):
if g is None or not (0 <= u < g.n and 0 <= v < g.n):
return False
return g.m[u][v] != 04.6 Impresión por consola
Mostrar la matriz ayuda a depurar. Usamos tabuladores para ver la estructura y opcionalmente pesos.
def imprimir_matriz(g):
if g is None:
return
encabezado = " " + "".join(f"{j:3d}" for j in range(g.n))
print(encabezado)
for i in range(g.n):
fila = "".join(f"{g.m[i][j]:3d}" for j in range(g.n))
print(f"{i:3d}{fila}")Ejemplo de uso completo:
g = crear_matriz(4)
if g is None:
raise SystemExit("No se pudo crear la matriz")
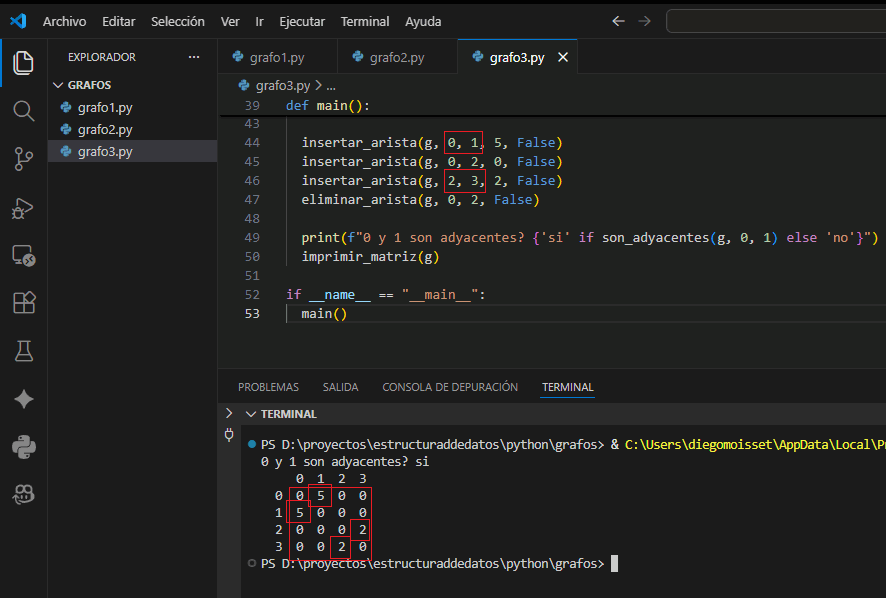
insertar_arista(g, 0, 1, 5, False)
insertar_arista(g, 0, 2, 0, False) # peso por defecto 1
insertar_arista(g, 2, 3, 2, False)
eliminar_arista(g, 0, 2, False)
print(f"0 y 1 son adyacentes? {'si' if son_adyacentes(g, 0, 1) else 'no'}")
imprimir_matriz(g)En la salida vemos la matriz actualizada tras insertar y eliminar aristas, y la verificación de adyacencia en O(1).
4.7 Aplicación completa para probar en VSCode
A continuación se muestra un archivo main.py autocontenido listo para ejecutar en VSCode. Incluye creación, inserción, eliminación, verificación e impresión.
class MatrizAdy:
def __init__(self, n):
self.n = n
self.m = [[0 for _ in range(n)] for _ in range(n)]
def crear_matriz(n):
if n <= 0:
return None
return MatrizAdy(n)
def insertar_arista(g, u, v, peso=1, es_dirigido=False):
if g is None or not (0 <= u < g.n and 0 <= v < g.n):
return
g.m[u][v] = peso if peso != 0 else 1
if not es_dirigido:
g.m[v][u] = g.m[u][v]
def eliminar_arista(g, u, v, es_dirigido=False):
if g is None or not (0 <= u < g.n and 0 <= v < g.n):
return
g.m[u][v] = 0
if not es_dirigido:
g.m[v][u] = 0
def son_adyacentes(g, u, v):
if g is None or not (0 <= u < g.n and 0 <= v < g.n):
return False
return g.m[u][v] != 0
def imprimir_matriz(g):
if g is None:
return
encabezado = " " + "".join(f"{j:3d}" for j in range(g.n))
print(encabezado)
for i in range(g.n):
fila = "".join(f"{g.m[i][j]:3d}" for j in range(g.n))
print(f"{i:3d}{fila}")
def main():
g = crear_matriz(4)
if g is None:
raise SystemExit("No se pudo crear la matriz")
insertar_arista(g, 0, 1, 5, False)
insertar_arista(g, 0, 2, 0, False)
insertar_arista(g, 2, 3, 2, False)
eliminar_arista(g, 0, 2, False)
print(f"0 y 1 son adyacentes? {'si' if son_adyacentes(g, 0, 1) else 'no'}")
imprimir_matriz(g)
if __name__ == "__main__":
main()Ejecuta este archivo en VSCode para observar la matriz y las operaciones básicas. Puedes variar el parámetro es_dirigido para probar grafos dirigidos y los valores de peso para simular grafos ponderados.