4 - Clasificación general de las estructuras de datos

Existen docenas de estructuras de datos, pero se agrupan en familias según su forma de organizar los elementos y las operaciones que priorizan. Conocer esta clasificación permite seleccionar rápidamente una opción viable antes de entrar en detalles de implementación.

En este tema repasamos cuatro grandes categorías: estructuras lineales, no lineales, basadas en hashing y estructuras avanzadas. Cada familia está vinculada con patrones de acceso característicos y compromisos entre velocidad, memoria y complejidad.

4.1 Estructuras lineales

Las estructuras lineales organizan los elementos en una sola dirección lógica. Cada dato tiene un anterior y un siguiente (excepto los extremos), lo que facilita recorridos secuenciales y operaciones que dependen de la posición.

4.1.1 Arrays

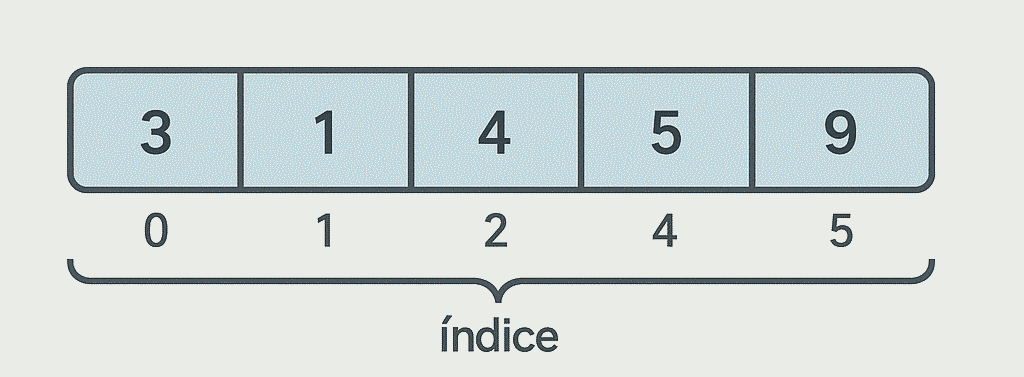
Un array (arreglo) almacena elementos en posiciones contiguas de memoria. Su ventaja principal es el acceso directo: conocer el índice permite leer o escribir en tiempo constante. Esto lo hace ideal para datos de tamaño fijo o cuando las lecturas superan ampliamente a las inserciones.

  • Ventajas: excelente localización en cache, simplicidad y soporte nativo en todos los lenguajes.
  • Desventajas: reubicar elementos al insertar en el medio y tamaño fijo en muchas plataformas (a menos que se use un array dinámico).
  • Casos de uso: tablas de puntuaciones, buffers de audio, representación de pixeles.
Representación simplificada de un array en memoria

4.1.2 Listas

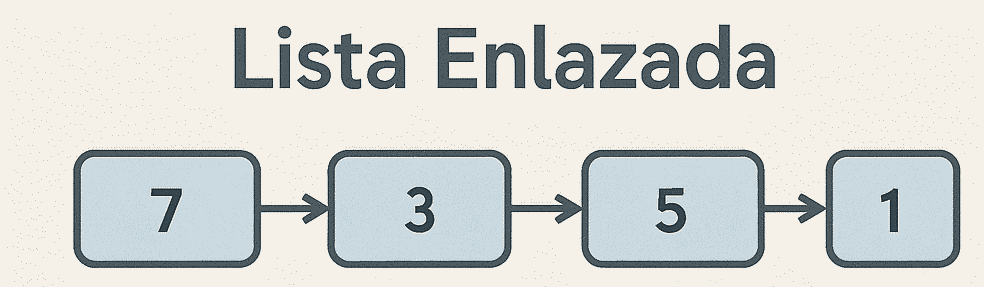
Una lista enlazada conecta nodos a través de referencias. Puede ser simple (sólo un enlace al siguiente), doble (enlaces al siguiente y anterior) o circular. Las listas permiten crecer de forma dinámica y realizar inserciones o eliminaciones sin mover grandes bloques.

  • Ventajas: inserción y eliminación eficientes en posiciones arbitrarias, eficiencia para estructuras que cambian continuamente.
  • Desventajas: acceso secuencial (no hay índices), mayor consumo de memoria por punteros adicionales.
  • Casos de uso: listas de reproducción, implementaciones de colas o pilas, sistemas donde el tamaño fluctúa constantemente.
Ilustración de una lista enlazada

4.1.3 Pilas

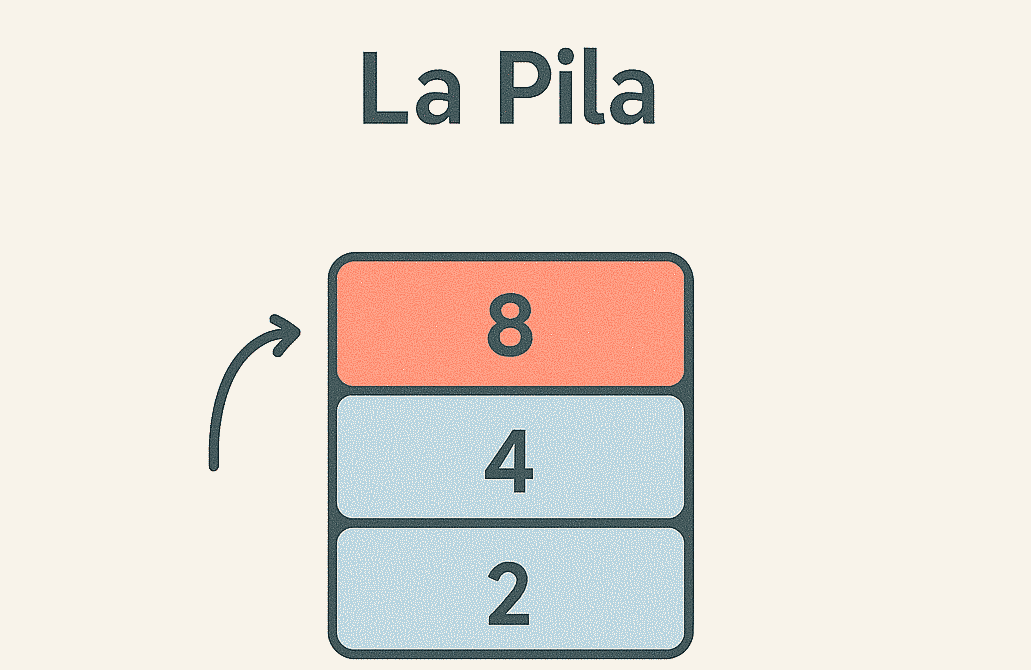
La pila es una estructura LIFO donde el último elemento insertado es el primero en salir. Se maneja con operaciones push (apilar) y pop (desapilar). Internamente puede basarse en un array o en una lista, pero el contrato LIFO siempre se mantiene.

  • Ventajas: implementaciones simples, operaciones constantes, ideal para mantener historiales.
  • Desventajas: no permite acceder a elementos intermedios sin desapilar.
  • Casos de uso: deshacer/rehacer, evaluación de expresiones, navegación por menús.
Funcionamiento de una pila LIFO

4.1.4 Colas

La cola es una estructura FIFO en la que el primer elemento que entra es el primero en salir. Se implementa comúnmente con arrays circulares o listas con referencias a la cabecera y la cola.

  • Ventajas: garantiza un orden justo, evita adelantos y facilita la programación de procesos asíncronos.
  • Desventajas: al igual que la pila, no permite saltos arbitrarios.
  • Casos de uso: planificación de tareas, colas de impresión, gestión de peticiones HTTP.
Funcionamiento de una cola FIFO

4.2 Estructuras no lineales

Las estructuras no lineales permiten que un elemento tenga múltiples relaciones con otros, formando jerarquías, redes o entramados complejos. Son apropiadas para representar dominios donde el orden secuencial no alcanza.

4.2.1 Árboles

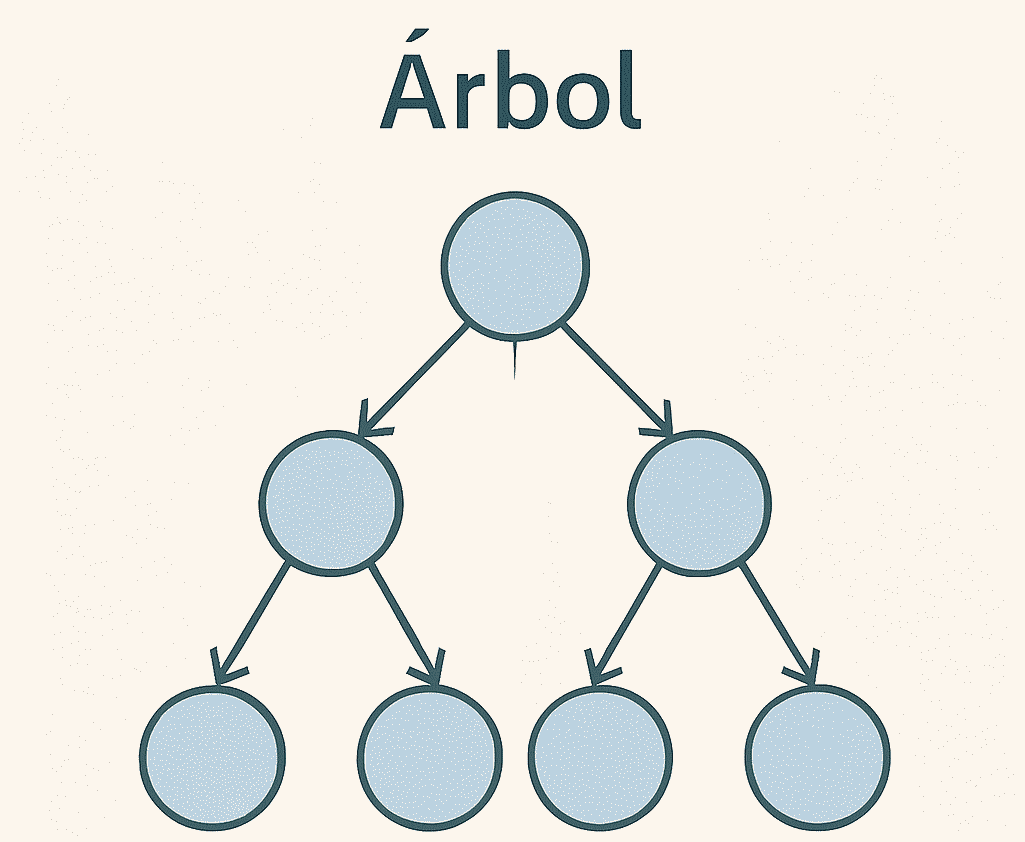
Un árbol es una colección de nodos conectados por aristas orientadas que parten de un nodo raíz. Cada nodo puede tener cero o más hijos, lo que permite modelar jerarquías como directorios, catálogos o decisiones.

  • Variantes: árboles binarios de búsqueda, árboles AVL, árboles B, árboles n-arios.
  • Ventajas: facilitan búsquedas logarítmicas cuando se mantienen balanceados, soportan recorridos ordenados y operaciones segmentadas.
  • Desafíos: mantener el balance, elegir la representación adecuada (punteros, arreglos, listas de hijos).
Estructura general de un árbol

4.2.2 Grafos

Un grafo consiste en un conjunto de vértices conectados mediante aristas. Puede ser dirigido o no dirigido, con pesos, etiquetas o restricciones específicas. Representa sistemas donde las relaciones importan tanto como los elementos.

  • Representaciones: lista de adyacencia, matriz de adyacencia, matrices dispersas.
  • Aplicaciones: redes sociales, mapas, diagramas de dependencias, circuitos.
  • Operaciones típicas: recorridos BFS/DFS, detección de ciclos, cálculo de caminos mínimos.
Grafo con nodos y aristas

4.2.3 Tries

Un trie es un árbol especializado para almacenar cadenas o secuencias donde cada nivel representa un carácter o elemento. Comparte prefijos y facilita búsquedas por coincidencia parcial, lo cual es crucial en sistemas de autocompletado o validación incremental.

  • Ventajas: permite encontrar prefijos comunes en tiempo proporcional a la longitud de la consulta, independientemente de la cantidad total de palabras.
  • Desventajas: consumo de memoria elevado si se almacenan pocos datos por rama.
  • Variantes: tries comprimidos, ternary search trees, DAWG (Directed Acyclic Word Graph).

4.3 Estructuras basadas en hashing

En lugar de depender del orden o de las relaciones jerárquicas, estas estructuras utilizan funciones matemáticas para transformar claves en posiciones de memoria. Buscan minimizar colisiones y proporcionar operaciones cercanas a tiempo constante.

4.3.1 Concepto de función hash

Una función hash toma una clave y genera un código numérico dentro de un rango fijo. Para que una estructura basada en hashing funcione, la función debe ser rápida de calcular y distribuir uniformemente las claves.

  • Propiedades deseadas: uniformidad, determinismo, baja probabilidad de colisiones.
  • Manejo de colisiones: encadenamiento (listas), direcciones abiertas, doble hashing.
  • Ejemplos: tablas hash, filtros probabilísticos, caches asociativos.

4.3.2 Mapas / Diccionarios

Los mapas o diccionarios almacenan pares clave-valor y permiten recuperar un elemento a partir de su clave en tiempo cercano a constante. En muchos lenguajes son la estructura por defecto para representar configuraciones, catálogos o resultados de consultas.

  • Ventajas: flexibilidad para claves arbitrarias, rendimiento estable aun con grandes volúmenes.
  • Desventajas: no preservan orden (a menos que se utilicen mapas ordenados basados en árboles).
  • Cuidados: elegir buenas funciones hash y dimensionar adecuadamente la tabla para evitar degradaciones.

4.4 Estructuras avanzadas (sin detalle, solo mención)

Cuando los requisitos son muy específicos (operaciones logarítmicas garantizadas, actualizaciones por rangos, consultas sobre subsecuencias), recurrimos a estructuras avanzadas. Aunque su implementación es más compleja, ofrecen garantías adicionales imprescindibles en algorítmica competitiva, motores de bases de datos o sistemas de tiempo real.

4.4.1 Heaps

Los heaps son arboles casi completos donde cada nodo mantiene una relación de prioridad respecto a sus hijos. Permiten obtener el máximo o mínimo en tiempo constante e insertar en tiempo logarítmico, lo que los vuelve ideales para colas de prioridad y algoritmos como Dijkstra.

4.4.2 Segment Trees

Los segment trees dividen un arreglo en segmentos o intervalos y almacenan información agregada de cada segmento (suma, mínimo, máximo). Hacen posible responder consultas sobre rangos y actualizar valores individuales en tiempo logarítmico.

4.4.3 Fenwick Trees

Tambien conocidos como Binary Indexed Trees, los Fenwick trees ofrecen una alternativa más ligera a los segment trees para consultas y actualizaciones de prefijos acumulados. Su implementación se apoya en operaciones bit a bit para determinar los intervalos relevantes.

4.4.4 Disjoint Set (Union-Find)

El Union-Find mantiene conjuntos disjuntos y soporta operaciones para unir conjuntos y encontrar el representante de cada elemento. Es crucial en algoritmos de componentes conectados o en la detección de ciclos.

Retornar