Hashing en C - Open Addressing

Direccionamiento abierto

En open addressing todas las entradas viven dentro del mismo array. Si un bucket esta ocupado, la estrategia de probing define la siguiente celda a inspeccionar hasta hallar un espacio libre (insercion) o la clave buscada (busqueda/eliminacion). Para sostener el tiempo promedio O(1) se necesita factor de carga bajo (usualmente < 0.7) y una funcion de exploracion que reduzca el clustering.

6.1 Concepto basico

Una colision no crea una lista adicional; se recorre el propio array siguiendo una secuencia deterministica. Cada intento i revisa una posicion distinta hasta encontrar una celda disponible.

6.2 Busqueda lineal (linear probing)

Explora celdas contiguas: idx = (h + i) % capacidad. Es simple y cache-friendly, pero sufre clustering primario: secuencias de ocupados crecen y atraen mas colisiones.

6.3 Busqueda cuadratica (quadratic probing)

La distancia crece cuadraticamente: idx = (h + i*i) % capacidad o (h + i*(i+1)/2) % capacidad. Dispersa mejor las colisiones cercanas y reduce el clustering primario. Requiere elegir una capacidad que garantice recorrer toda la tabla (frecuente usar numeros primos y reinsercion al rebasar cierto factor de carga).

6.4 Doble hashing (double hashing)

Usa dos funciones: idx = (h1 + i * h2) % capacidad. El paso h2 debe ser distinto de 0 y coprimo con la capacidad (por ejemplo, h2 = 1 + (clave % (capacidad - 1))). Minimiza tanto clustering primario como secundario y distribuye mejor las sondas.

6.5 Manejo de celdas ocupadas y celdas borradas

Vacia: nunca tuvo un elemento; detiene la busqueda.
Ocupada: almacena clave y valor.
Borrada: contiene un marcador; permite continuar el probing en busquedas, pero habilita reutilizar el espacio en inserciones.

Sin el estado “borrada” la eliminacion romperia la cadena de sondas y haria inaccesibles algunas claves.

6.6 Problema del clustering

Primario: secuencias contiguas crecen con linear probing. Secundario: ocurre cuando muchas claves comparten la misma secuencia de sondas (afecta linear y quadratic). Mitigacion: reducir factor de carga, usar quadratic o doble hashing, y rehashing preventivo.

6.7 Insercion

Se calcula el indice base, se recorre la secuencia de probing hasta encontrar una celda vacia o borrada. Si se encuentra la clave, se actualiza el valor; si no, se escribe en la primera celda disponible.

typedef enum { CELDA_VACIA, CELDA_OCUPADA, CELDA_BORRADA } Estado;

typedef struct {
  const char *clave;
  int valor;
  Estado estado;
} Entrada;

static unsigned long hash1(const char *clave, unsigned long cap);
static unsigned long hash2(const char *clave, unsigned long cap);

int insertar(Entrada *tabla, unsigned long cap, const char *clave, int valor) {
  unsigned long base = hash1(clave, cap);
  unsigned long paso = hash2(clave, cap);
  long primera_borrada = -1;
  for (unsigned long i = 0; i < cap; i++) {
    unsigned long idx = (base + i * paso) % cap; /* doble hashing */
    if (tabla[idx].estado == CELDA_OCUPADA && strcmp(tabla[idx].clave, clave) == 0) {
      tabla[idx].valor = valor; /* actualizar */
      return 1;
    }
    if (tabla[idx].estado == CELDA_BORRADA && primera_borrada == -1) primera_borrada = (long)idx;
    if (tabla[idx].estado == CELDA_VACIA) {
      unsigned long destino = (primera_borrada != -1) ? (unsigned long)primera_borrada : idx;
      tabla[destino].clave = clave;
      tabla[destino].valor = valor;
      tabla[destino].estado = CELDA_OCUPADA;
      return 1;
    }
  }
  return 0; /* tabla llena */
}

6.8 Busqueda

El recorrido sigue la misma secuencia usada para insertar. Se detiene al encontrar una celda vacia (la clave no esta) o la coincidencia exacta.

Entrada *buscar(Entrada *tabla, unsigned long cap, const char *clave) {
  unsigned long base = hash1(clave, cap);
  unsigned long paso = hash2(clave, cap);
  for (unsigned long i = 0; i < cap; i++) {
    unsigned long idx = (base + i * paso) % cap;
    if (tabla[idx].estado == CELDA_VACIA) return NULL;
    if (tabla[idx].estado == CELDA_OCUPADA && strcmp(tabla[idx].clave, clave) == 0) return &tabla[idx];
  }
  return NULL;
}

6.9 Eliminacion

Se busca la clave y, si se encuentra, la celda se marca como borrada. No se puede marcar como vacia porque cortaria el recorrido de otras claves que colisionaron.

int eliminar(Entrada *tabla, unsigned long cap, const char *clave) {
  Entrada *e = buscar(tabla, cap, clave);
  if (!e) return 0;
  e->estado = CELDA_BORRADA;
  return 1;
}

6.10 Comparacion entre metodos

Metodo	Formula de probing	Ventajas	Riesgos
Linear probing	(h + i) % cap	Implementacion sencilla, excelente localidad de cache	Clustering primario intenso; sensible a factores de carga altos
Quadratic probing	(h + i*i) % cap	Reduce clustering primario, recorridos mas cortos	Requiere reglas sobre cap para cubrir todas las celdas
Doble hashing	(h1 + i*h2) % cap	Mejor dispersion, mitiga clustering primario y secundario	Necesita dos funciones hash y cap primo/coprimo con h2

En la practica: linear probing es ideal con tablas mas grandes que el numero esperado de elementos y lecturas frecuentes; quadratic probing evita clusters grandes con pocos cambios; doble hashing ofrece la mejor distribucion a costa de dos funciones y mas cuidado al elegir la capacidad.

6.11 Programa completo para probar en CLion (open addressing con doble hashing)

Compila este programa en CLion para ver inserciones, busquedas y eliminaciones usando direccionamiento abierto con doble hashing y manejo de celdas vacias/borradas.

#include <stdio.h>
#include <stdlib.h>
#include <string.h>

typedef enum { CELDA_VACIA, CELDA_OCUPADA, CELDA_BORRADA } Estado;

typedef struct {
  const char *clave;
  int valor;
  Estado estado;
} Entrada;

typedef struct {
  Entrada *celdas;
  unsigned long capacidad;
  unsigned long cantidad;
} HashOA;

static unsigned long hash1(const char *clave, unsigned long cap) {
  unsigned long h = 5381;
  int c;
  while ((c = *clave++) != 0) {
    h = ((h << 5) + h) + (unsigned long)c; /* djb2 */
  }
  return h % cap;
}

static unsigned long hash2(const char *clave, unsigned long cap) {
  /* paso distinto de 0 y coprimo con cap */
  unsigned long h = 0;
  int c;
  while ((c = *clave++) != 0) {
    h = h * 131 + (unsigned long)c;
  }
  return 1 + (h % (cap - 1));
}

HashOA *hash_crear(unsigned long capacidad) {
  HashOA *t = malloc(sizeof(HashOA));
  t->capacidad = capacidad;
  t->cantidad = 0;
  t->celdas = malloc(sizeof(Entrada) * capacidad);
  for (unsigned long i = 0; i < capacidad; i++) {
    t->celdas[i].estado = CELDA_VACIA;
    t->celdas[i].clave = NULL;
    t->celdas[i].valor = 0;
  }
  return t;
}

Entrada *hash_buscar(HashOA *t, const char *clave) {
  unsigned long base = hash1(clave, t->capacidad);
  unsigned long paso = hash2(clave, t->capacidad);
  for (unsigned long i = 0; i < t->capacidad; i++) {
    unsigned long idx = (base + i * paso) % t->capacidad;
    if (t->celdas[idx].estado == CELDA_VACIA) return NULL;
    if (t->celdas[idx].estado == CELDA_OCUPADA && strcmp(t->celdas[idx].clave, clave) == 0) {
      return &t->celdas[idx];
    }
  }
  return NULL;
}

int hash_insertar(HashOA *t, const char *clave, int valor) {
  unsigned long base = hash1(clave, t->capacidad);
  unsigned long paso = hash2(clave, t->capacidad);
  long primera_borrada = -1;
  for (unsigned long i = 0; i < t->capacidad; i++) {
    unsigned long idx = (base + i * paso) % t->capacidad;
    if (t->celdas[idx].estado == CELDA_OCUPADA && strcmp(t->celdas[idx].clave, clave) == 0) {
      t->celdas[idx].valor = valor; /* actualizar */
      return 1;
    }
    if (t->celdas[idx].estado == CELDA_BORRADA && primera_borrada == -1) primera_borrada = (long)idx;
    if (t->celdas[idx].estado == CELDA_VACIA) {
      unsigned long destino = (primera_borrada != -1) ? (unsigned long)primera_borrada : idx;
      t->celdas[destino].clave = clave;
      t->celdas[destino].valor = valor;
      t->celdas[destino].estado = CELDA_OCUPADA;
      t->cantidad++;
      return 1;
    }
  }
  return 0; /* tabla llena */
}

int hash_eliminar(HashOA *t, const char *clave) {
  Entrada *e = hash_buscar(t, clave);
  if (!e) return 0;
  e->estado = CELDA_BORRADA;
  t->cantidad--;
  return 1;
}

void hash_imprimir(HashOA *t) {
  for (unsigned long i = 0; i < t->capacidad; i++) {
    if (t->celdas[i].estado == CELDA_OCUPADA) {
      printf("[%lu] (%s -> %d)\n", i, t->celdas[i].clave, t->celdas[i].valor);
    } else if (t->celdas[i].estado == CELDA_BORRADA) {
      printf("[%lu] \n", i);
    } else {
      printf("[%lu] \n", i);
    }
  }
}

void hash_destruir(HashOA *t) {
  free(t->celdas);
  free(t);
}

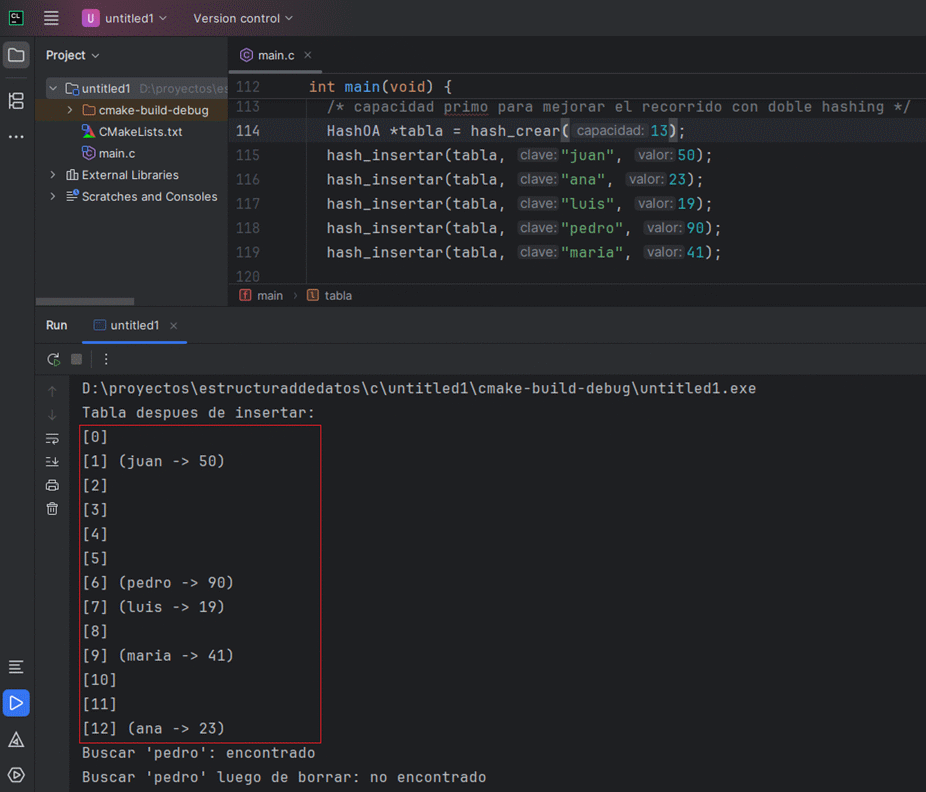
int main(void) {
  /* capacidad primo para mejorar el recorrido con doble hashing */
  HashOA *tabla = hash_crear(13);
  hash_insertar(tabla, "juan", 50);
  hash_insertar(tabla, "ana", 23);
  hash_insertar(tabla, "luis", 19);
  hash_insertar(tabla, "pedro", 90);
  hash_insertar(tabla, "maria", 41);

  printf("Tabla despues de insertar:\n");
  hash_imprimir(tabla);

  Entrada *resultado = hash_buscar(tabla, "pedro");
  printf("Buscar 'pedro': %s\n", resultado ? "encontrado" : "no encontrado");

  hash_eliminar(tabla, "pedro");

  resultado = hash_buscar(tabla, "pedro");
  printf("Buscar 'pedro' luego de borrar: %s\n", resultado ? "encontrado" : "no encontrado");

  printf("Tabla final:\n");
  hash_imprimir(tabla);

  hash_destruir(tabla);
  return 0;
}

Ejecutalo y observa el probing generado por el doble hashing, incluyendo celdas marcadas como borradas para preservar la cadena de busqueda.

[0]

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

Tabla vacia con 13 celdas; lista para insertar.

Capacidad = 13 hash1: djb2 hash2: 1 + (h % 12) Formula de probing: (h1 + i * h2) % 13

Visualizacion de direccionamiento abierto y doble hashing — Distribucion de claves con direccionamiento abierto y doble hashing.

Retornar

6 - Direccionamiento abierto (Open Addressing)